Çemberin karesini alma

Kare ve dairenin alanı aynıdır.

Dairenin kare alma a, klasik bir sorun bir geometri . İştir inşa etmek bir kare ile aynı bölgede belirli bir mesafede çember içinde sonlu sayıda adımda . Bu bir eşdeğer sözde dairenin düzeltilmesi , yani düz bir yapımı, hat olduğu karşılık gelir çevresi daire . Bu yapımıyla dönüş tekabül olarak çevrelerinde sayısına segmentinden (yarı çevresi), uzunluğu birimi ile aynı  uzunlukta . Bire inşaat araçları kısıtladığında yöneticilerin ve pergel , görevdir çözülemeyen nedeniyle aşkınlık içinde . 1882 yılına kadar Alman matematikçi Ferdinand von Lindemann bunu kanıtlayamadı . ${\ görüntü stili \ pi}$${\ görüntü stili 1}$ ${\ görüntü stili \ pi}$

Çemberin karesini almak matematikteki en popüler problemlerden biridir. Yüzyıllar boyunca sadece matematikçiler değil, sıradan insanlar da boş yere çözüm aradılar. Çemberin karesini alma terimi , birçok dilde çözülemeyen bir görev için bir metafor haline geldi .

Öykü

tarih öncesi

Ahmes tarafından Rhind papirüsünde kullanılan yaklaşıklık yöntemi :
Kenar uzunluğu 9 olan bir karede 9 çapında bir daire, kenar uzunluğu 3 olan dokuz küçük kareye bölünmüştür.
Dairenin alanı kabaca (düzensiz) bir sekizgenin (7 × 9) ve daha kesin olarak kenar uzunluğu 8 (64) olan bir karenin alanına karşılık gelir.

Eski doğu uygarlıklarında dairesel alanları hesaplamak için yöntemler zaten vardı. Örneğin, Rhind papirüsünde (MÖ 1650 civarında) dairenin çapı 9 parçaya bölünmüştür. Bu birimlerdeki tam alanı . Bu değer daha sonra kenar uzunluğu 8 olan bir kare ile, yani . İkinci bir yöntemde, daire düzensiz bir sekizgenle yaklaştırılır. Bu amaçla, yazılı olduğu 9×9 kareden toplam alanı 18 birim olan eş üçgenler kesilerek 63 tane kalır. Bu tür örnek çözümler uygulamadan elde edilmiş ve uygulamaya yöneliktir, başka teorik değerlendirmeler yapılmamıştır, özellikle kesin çözüm ve yaklaşıklık arasında bir ayrım yapılmamıştır.${\ displaystyle {\ tfrac {\ pi} {4}} \ cdot 9 ^ {2} = 63 {,} 62 \ ldots}$${\ displaystyle 8 ^ {2} = 64}$

Bir tümdengelim içinde yaklaşım matematik ettiği, kanıta dayalı önermeler itibaren M.Ö. 6. yüzyılda geliştirilen örnek sorunları yerine,. Yunanistan'da. Bir dereceye kadar zaten Miletoslu Thales ile birlikte , açıkça Sisamlı Pisagor'un kurduğu Pisagor Okulu'nu tanıdı. MÖ 6. yüzyılın sonlarında veya 5. yüzyılın başlarında, genellikle Metapontium'un Pisagor Hippasus'una atfedilen kıyaslanamaz uzantıların keşfi ile . Bu olduğu ortaya çıktı inşa edilebilir bir tamsayıdır oranı olarak ifade edilemez (bir kare çapraz örneğin) nesneler. Bilinen tek sayı türleri tam sayılar ve tam sayıların oranları (bugünkü tabirle "rasyonel sayılar") olduğundan, bu dikkat çekici görünüyordu. Herhangi bir geometrik çizginin buna göre ölçülebilir olması gerekiyordu, yani birbirlerine tamsayı uzunluk oranlarına sahip olmaları gerekiyordu. Keşfin bir sonucu olarak, önceki anlamda bir “sayı” olarak aritmetik olarak temsil edilemeyen uzunluklar artık geometrik olarak oluşturulabildi (bugünkü tabirle “irrasyonel sayılar” meselesidir). Geometri birdenbire aritmetiğin yapabileceğinden fazlasını temsil edebilir. Bu keşfin bir sonucu olarak, aritmetik geometri lehine bir arka koltuk aldı, denklemlerin artık geometrik olarak çözülmesi gerekiyordu, örneğin şekilleri yan yana koyarak ve farklı şekilleri dikdörtgen veya karelere dönüştürerek. Üç klasik yapı sorunları arasında geç 5. yüzyıldan kalma, daire, görevi kare alma yanında antik matematik tarihine üçe açısını bölünmesi ve Deliç sorununu küpü iki katına.

İnşaat araçlarını pergel ve cetvellerle sınırlamak için genel bir gereklilik yoktu. Klasik problemlerle uğraşırken, erkenden gelişmiş araçlara dayalı çözümler bulundu. Ancak zamanla, mümkün olan en büyük kısıtlamayı gerektiren bir tutum ortaya çıktı. En geç Pappos tarafından bu en kapsamlı kısıtlama bir önlem haline geldi.

Erken iş

Yunan yazar Plutarch'a göre, filozof Anaxagoras "dairenin karesini hapishanede yazan (veya: çizilmiş, eski Yunan ἔγραφε )" ilk kişilerden biriydi . Plutarch, Anaxagoras'ın yapısı hakkında daha fazla ayrıntı sağlamaz. Anaksagoras yaklaşık MÖ 430'da hapishanede kalacaktı. Filozof Atina'da tanrısızlıkla suçlandığında .

Araştırmanın başlangıcından Daha ayrıntılı kaynaklar çoğunlukla arasında çalışmasını yorumlayan gelen Aristo Geç Antik arayla 900 yıl yaklaşık yazılmıştır, yani yazıları. İlk yaklaşımların kronolojik sırası ve kesin düşünce süreçleri buna göre belirsizdir. MÖ 5. yüzyılın en önemli eserleri M.Ö. Sakızlı Hipokrat , Antiphon , Herakleialı Bryson ve Elisli Hippias'tan gelmektedir .

"Hipokrat'ın küçük ayı": Gri "küçük ayın" alanı, ABC dik açılı üçgeninin alanına karşılık gelir.

Üçgenlerin dikdörtgenlere, dikdörtgenlerin karelere dönüştürülmesi (dikdörtgenin karesini alma ) veya iki karenin eklenmesi ( Pisagor teoremi ) zaten temel olarak bilinen geometrik teoremlerle öğrenilebilirdi. Sakızlı Hipokrat, MÖ 440 civarında olabilir. BC, tam olarak kareye dönüştürülebilen eğrisel olarak sınırlandırılmış bir alan örneği verir. Bir dairenin benzer bölümlerinin alanlarının, kirişlerinin üzerindeki kareler gibi davrandığına dair hâlâ kullandığı aksiyomu temel alan Hipokrat, " Hipokrat'ın küçük ayı " olarak adlandırılan dairesel yaylarla sınırlanan alanların karesini almayı başardı . Bununla birlikte, dairenin karesi bu şekilde elde edilemez, çünkü yalnızca belirli ayların karesi alınabilir - örneğin karenin kenarının üzerindekiler, ancak normal bir altıgenin kenarının üzerindekiler değil - karesi alınabilir.

Üçgenlerin (ve dolayısıyla herhangi bir çokgenin) kareye dönüştürülebilmesi gerçeği, daire ile aynı alana sahip bir çokgen oluşturmak için ikinci bir yaklaşımdı. Antiphon, daireye yazılı çokgenlerle yaklaşma fikrine sahipti. Herakleia'lı Bryson, bu prosedürü ek olarak sınırlandırılmış çokgenlerle daireye yaklaştırarak ve bir ara değer oluşturarak geliştirdi.

Hippias von Elis MÖ 425 civarında gelişti Açısal üç bölümü çözmek için, dairesel bir doğrusal hareketle üst üste bindirilerek mekanik olarak oluşturulan bir eğri. Yüz yıl kadar sonra, Deinostratos , kuadratrik olarak adlandırılan bu eğrinin yardımıyla , uzunluk çizgisinin - ve dolayısıyla alanı olan bir karenin  - diğer temel yapıların yardımıyla inşa edilebileceğini keşfetti . Bununla birlikte, kuadratrisin kendisi aşkın bir eğri olduğu için (bkz . imkansızlığın kanıtı ), yani bir pusula ve cetvel ile oluşturulamadığından, tam anlamıyla çözüme ulaşılamadı.${\ görüntü stili 2 / \ pi}$${\ görüntü stili \ pi}$

Arşimet

Spiral yardımıyla daire kareleme: A, spiralin ilk dönüşten sonra ulaştığı O kaynağı etrafındaki noktasını belirtir. Bu noktada sarmalın teğeti B'deki OA'ya dik olanla kesişir. Arşimet'e göre, BO segmenti OA yarıçaplı dairenin çevresine eşittir, dolayısıyla kırmızı dairenin alanı, alanına eşittir. mavi üçgen.

Başlıklı ayrıntılı bir tez Dairesel Ölçüm gelip vardır bize aşağı gelen Arşimed . Arşimet bu çalışmada üç temel teoremi kanıtladı:

1. Bir dairenin alanı, daire yarıçapı bir ve çevresi diğer bacak olan bir dik üçgenin alanına eşittir . Dairenin alanı ½ · yarıçap · çevre olarak hesaplanabilir.
2. Bir dairenin alanı neredeyse çapının karesi ile ilişkilidir ¹¹ / ₁₄ .
3. Bir dairenin çevresi çapın 3+ ¹⁰ / _{71'inden büyük} ve 3 + ¹⁰ / _70'inden küçüktür.

İlk cümleyle, dairenin karesini alma sorunu, verilen yarıçaptan bir dairenin çevresinin oluşturulabilirliği ve dolayısıyla . Üçüncü sette Arşimet, bu sayının kolay ve doğru bir yaklaşıklığına eşitti, yani ²² / ₇ , pratik amaçlar için hala kullanılan bir değer (≈ 3.143). İkinci hareket, diğer ikisinden basit bir sonuçtur ; bir dairenin alanı, çapının karesiyle orantılıdır ve Öklid tarafından zaten biliniyordu. Arşimet burada orantı sabitinin değerini verdi. ${\ görüntü stili \ pi}$

İfadelerini kanıtlamak için Arşimet, yazılı ve sınırlandırılmış düzenli çokgenlerle dairenin herhangi bir yaklaşımının elde edilebileceği Herakleia'nın Bryson fikrini çizdi . Arşimet, yazılı altıgen ve çevrelenmiş üçgenden başlayarak sayfa sayısını art arda ikiye katlayarak 96 kenara ulaştı. Bireysel hesaplama adımlarında meydana gelen kareköklerin akıllıca bir tahmini, cümle 3'te belirtilen sınırlarla sonuçlandı.

Spiraller üzerine başka bir çalışmada , Arşimet , Hippias'ın dörtgeni gibi, doğrusal bir hareketle bir dairesel üst üste bindirilerek elde edilen Arşimet spiralinin yapımını tanımladı . Bu spirale teğet uygulayarak, bir dairenin çevresinin düz bir çizgi üzerinde çıkarılabileceğini gösterdi. Daha sonra yorumcular dairenin karesini almak için yapılan hazırlık çalışmalarına işaret ederken, Arşimet'in kendisi bir açıklama yapmadı. Ancak Quadratrix'te olduğu gibi, ne spiralinin kendisi ne de tanjantı bir pusula ve cetvelle oluşturulamaz.

orta Çağ

Franco von Liège tarafından dairenin kare şekli: Franco, daireyi bir dikdörtgen oluşturmak için bir araya getirdiği 44 sektöre böler.

Yaklaşık 11. yüzyıldan itibaren Hıristiyan Avrupa'da antik matematiğe artan ilginin bir sonucu olarak, çemberin karesi üzerine bir dizi inceleme ortaya çıktı, ancak gerçek çözüme önemli katkılarda bulunmadı. Arşimed Yaklaşım Ortaçağ'da bir adım geriye doğru olarak kabul edilecek mi ²² / ₇ daire sabiti için uzun tam olarak kabul oldu.

Orta Çağ'ın dairesel kareleme problemini yeniden ele alan ilk yazarlarından biri Franco von Liège idi . De quadratura circuli adlı eseri 1050 civarında yazılmıştır. Franco önce reddettiği üç kareyi sunar. İlk iki seçenek , kenar uzunluğu kare ⁷ / ₈ veya çapraz için ¹⁰ / ₈ daire çapı olan 3 nispeten düşük yaklaşımları ¹ / ₁₆ ve 3 ¹ / ₈ için eşdeğeri. Üçüncü öneri, sırayla, karenin çevresini dairenin çevresiyle eşitler ve böylece ikincisinin düzeltilmesini gerektirir. ${\ görüntü stili \ pi}$

Franco'nun kendi çözümü, çapı 14 olan bir daireye dayanmaktadır. Oturduğu alan tam olarak 7² × ²² / ₇  = 154. Franco'nun akıl karekökü ile aynı kare find yüz değil hesaplanabilir sonra ²² / ₇ geometrik constructible incommensurable mesafe gibi (bkz akıldışıdır geçmişini ama karekök) teslim ²² / ₇ squaring. Bunu yapmak için, daireyi 11 ve 14 kenarları olan bir dikdörtgen oluşturmak üzere birleştirdiği 44 eşit sektöre böler . Ancak Franco, dairesel sektörleri 1 ve 7 uzunluğunda katetlerle dik açılı üçgenlerle değiştirdiği gerekli hileyi açıklamaz. Başka bir sorun, dikdörtgeni uygun bir ayrıştırma yoluyla kareye dönüştürme girişiminin başarısız olmasıdır. Açıkçası Franco, geleneksel Yunan sürecine aşina değildi.

Skolastisizm üzerine daha sonraki incelemeler , iyi bilinen klasiklerin argümanlarını tartmak için az ya da çok tükenmiştir. Sadece Orta Çağ'ın sonlarında Arşimet'in yazılarının Latince çevirilerinin yayılmasıyla , değer ²² / _{7 olarak} kabul edildi ve Cusa'lı Nicholas gibi soruna yeni çözümler aradı . Çemberi, artan sayıda kenarı olan bir dizi düzenli çokgenle yaklaşma fikrini benimsedi, ancak Arşimet'in aksine çevreyi belirlemeye çalışmadı, daha ziyade çokgenlerin belirli bir sabit çevresi ile daire yarıçapını belirlemeye çalıştı. . Von Kues , doktor ve doğa bilimci Paolo Toscanelli'ye yazdığı bir mektupta , doğru olduğunu düşündüğü böyle bir çözüm sundu. Daire numarası için elde edilen değer en az Arşimet tarafından verilen sınırlar arasındadır. Kues'in konuyla ilgili gerçek çalışması, önemli ölçüde daha zayıf yaklaşımlar sağlar ve bu nedenle , hesaplamaların yanlışlığını gösteren ve kanıtları "felsefi, ancak matematiksel değil" olarak nitelendiren Regiomontanus tarafından bir polemiğin hedefi haline geldi .

Erken modern dönemde dairesel ölçümdeki gelişmeler

16. yüzyıldan itibaren, Arşimet yaklaşım yönteminin daha da geliştirilmesi ve modern analitik yöntemlerin ortaya çıkması, daire hesaplamasında ilerlemeler getirdi.

Orijinal Arşimet yönteminde, bir dairenin çevresi, daireye yazılan bir çokgenin çevresi ve daire tarafından çevrelenen bir çokgenin çevresi ile tahmin edilir. Daha kesin sınırlar, köşe sayısındaki artıştan kaynaklanır. Hollandalı matematikçi Willebrord van Roijen Snell ( Snellius ), sayfa sayısını artırmadan, bir yayın uzunluğu için sadece çokgenlerin kirişlerinden daha ince sınırların belirlenebileceğini buldu. Ancak bu sonucu kesin olarak kanıtlayamadı. Christiaan Huygens , Snellius tarafından kurulan teoremleri de kanıtladığı De circuli magnitudine inventa adlı çalışmasında Snellian yaklaşımı geliştirdi ve geliştirdi . Huygens, tamamen basit bir geometrik yolla, çokgen ile daire arasındaki alanı o kadar iyi sınırlamayı başardı ki, çokgenlerin karşılık gelen kenar sayısı verildiğinde, dairelerin sayısını Arşimet'in en az dört katı ondalık basamak aldı. ' yöntem.

Dairesel sabiti belirlemeye yönelik tamamen geometrik yaklaşım, Huygens'in çalışmasıyla esasen tükendi. Sonsuz seriler , özellikle trigonometrik fonksiyonların seri açılımları yardımıyla daha iyi yaklaşımlar elde edildi . François Viète , 16. yüzyılın sonunda, ardışık çokgenlerin belirli yol koşullarını göz önünde bulundurarak sonsuz bir çarpımın ilk tam temsilini zaten bulmuş olmasına rağmen , bu formülün hantal olduğunu kanıtladı. John Wallis'den sadece çarpma ve bölme gerektiren daha basit bir seri geliyor , William Brouncker'dan daire sayısının sürekli bir kesir olarak başka bir temsili . Uygulama için daha önemli olan, James Gregory tarafından ve Gottfried Wilhelm Leibniz'den bağımsız olarak bulunan arktanjant dizisiydi . Bu dizi kendisi yalnızca rağmen yakınsayan yavaş , diğer seri da çevrelerinin sayısını hesaplamak için çok uygun olan, bunun elde edilebilir. 18. yüzyılın başında bu tür seriler yardımıyla 100'den fazla basamak hesaplandı, ancak dairesel kareleme problemi hakkında yeni bilgiler elde edilemedi. ${\ görüntü stili \ pi}$${\ görüntü stili \ pi}$

Cebirsel problem ve mantıksızlığı ${\ görüntü stili \ pi}$

Géométrie Descartes'ın başında analitik geometrinin yeni yaklaşımını anlatıyor .

Oronce Fine , Quadratura circuli , 1544.

JP de Fauré , tez, découverte, et gösterileri de la quadrature matematiği du cercle , 1747.

Problemi çözmek için, bir yandan geometrik "inşa edilebilir" terimine cebirsel bir anlam vermek, diğer yandan daire numarasının özelliklerine daha yakından bakmak gerekiyordu.

Pergel ve cetvelli geometrik bir yapı, sonlu sayıda verilen noktalara dayanır ve iki düz çizgiyi, iki daireyi veya bir düz çizgiyi bir daireyle keserek sonlu sayıda adımda yeni noktalar belirler. Bu işlemin cebir diline çevirisi , 17. yüzyılda Pierre de Fermat ve René Descartes tarafından ağırlıklı olarak geliştirilen analitik geometri çerçevesinde koordinat sistemlerinin tanıtılmasıyla sağlandı . Yeni araçlarla, düz çizgiler ve daireler denklemlerle tanımlanabilir, denklem sistemleri çözülerek kesişmeler belirlenebilir. 1 uzunluğundaki bir doğruya göre pergel ve cetvelle oluşturulabilecek doğru uzunluklarının, sonlu sayıda rasyonel (temel) işlemlerden (toplama, çıkarma, çarpma ve bölme) kaynaklanan sayılara tam olarak karşılık geldiği ortaya çıktı ve sonlu bir sayı Kare alma işleminin tersinden elde edilen 1 sayısının kareköklerinin sayısını elde edin. Özellikle, bu uzunluklar cebirsel sayılara karşılık gelir , yani rasyonel katsayılarla herhangi bir derecede cebirsel denklemin bir çözümü olan sayıların bir alt kümesidir . Cebirsel olmayan sayılara transandant denir . Buna göre, uzunluk 1'den başlayan aşkın uzunluklar, bir pergel ve cetvelle sonlu sayıda adımda oluşturulamaz.

Daire numarasının daha fazla araştırılması için başlangıç ​​noktası, Leonhard Euler'in 1748'de Introductio in analysin infinitorum adlı çalışmasında yayınladığı bazı temel bulgulardı . Diğer şeylerin yanı sıra , Euler kendi adını taşıyan Euler formülünü kullandı.

${\ displaystyle e ^ {i \, z} = \ cos z + ben \ günah z}$

Trigonometrik fonksiyonlar ile üstel fonksiyon arasında ilk kez bir bağlantı kurmuş ve daha sonra kendi adıyla anılacak olan Euler sayısı e'nin bazı devam eden kesir ve seri gösterimlerini sağlamıştır .${\ görüntü stili \ pi}$

Johann Heinrich Lambert , Euler'in 1766'da devam eden kesir gelişmelerinden birinin yardımıyla ilk kez e ve irrasyonel sayıları, yani bir tamsayı kesir tarafından temsil edilemeyen sayıları gösterebilen bu ön çalışmadan yararlandı . Lambert'in argümanındaki küçük bir boşluk, 1806'da , aynı zamanda mantıksızlığın kanıtını sunan Adrien-Marie Legendre tarafından kapatıldı .${\ görüntü stili \ pi}$ ${\ görüntü stili \ pi ^ {2}}$

Cebirsel olmayabilecek varsayım , en azından Euler, Lambert ve Legendre tarafından dile getirildi. Ancak 19. yüzyılın ortalarına kadar aşkın sayıların olması gerektiği henüz net değildi. Bu kanıt, 1844/1851'de Joseph Liouville tarafından aşkın Liouville sayılarının açık bir şekilde oluşturulması yoluyla elde edildi .${\ görüntü stili \ pi}$

imkansızlığın kanıtı

Ferdinand von Lindemann nihayet 1882'de cebirsel değil aşkın olduğunu kanıtlayabildi . Bu nedenle düz bir çizgi oluşturmak mümkün değildir ve dairenin karesini almak imkansızdır.${\ görüntü stili \ pi}$${\ görüntü stili \ pi}$

Lindemann, çalışmasında Fransız matematikçi Charles Hermite'nin bir sonucunu kullandı . 1873'te Euler'in  e sayısının aşkın olduğunu göstermişti. Buna dayanarak, Lindemann, birbirinden farklı herhangi bir cebirsel sayı ve herhangi bir cebirsel sayı için denklemin aşağıdaki gibi olduğunu söyleyen Lindemann-Weierstrass teoremini kanıtlamayı başardı.${\ displaystyle z_ {1}, \ noktalar, z_ {r}}$${\ görüntü stili n_ {1}, \ nokta, n_ {r}}$

${\ displaystyle \ toplam _ {i = 1} ^ {r} n_ {i} e ^ {z_ {i}} = 0}$

yalnızca tümü sıfır değerine sahipse uygulanabilir . Özellikle, ifade sıfır dışında herhangi bir cebirsel sayı z için rasyonel bir sayı veremez  . Bu hazırlıktan sonra Lindemann, Euler'in kimliğinin yardımıyla cebirsel olduğu varsayımıyla çelişmeyi başardı ; bu yüzden aşkın olması gerekiyordu.${\ görüntü stili n_ {i}}$${\ görüntü stili e ^ {z}}$${\ görüntü stili \ pi}$ ${\ displaystyle e ^ {i \ pi} = - 1}$${\ görüntü stili \ pi}$

Lindemann'ın aşkınlığının kanıtı , sonraki yıllarda ve on yıllarda, örneğin 1893'te David Hilbert tarafından önemli ölçüde basitleştirildi .${\ görüntü stili \ pi}$

Dairesel karelemenin popülerliği

Diğer birkaç soru gibi, çemberin karesi de matematiğin dışında büyük popülerlik kazandı. Sonuç olarak, birçok matematiksel meslekten olmayan kişi, görünüşte basit olan sorunu çözmeye çalıştı; bazıları onları bulduklarına inanıyordu.

18. ve 19. yüzyıllarda giderek artan amatör çalışma hacmine ilişkin raporlar ve konuyla ilgili örnekler Jean-Étienne Montucla , Johann Heinrich Lambert ve Augustus de Morgan'da bulunabilir . Kural olarak bunlar, problemin "tam olarak" mekanik, sayısal veya geometrik bir yaklaşım yapısı aracılığıyla çözüldüğü süreçlerdi. Bu tür çalışmalar o kadar çok sayıda matematikçiye veya bilimsel kuruma sunuldu ki, örneğin 1775'te Paris Bilimler Akademisi , dairesel karelemenin sözde çözümlerinin daha fazla araştırılmasını resmen reddetmek zorunda hissetti:

Lindemann'ın 1882'deki imkansızlık ispatından sonra bile, 20. yüzyılda, daha yakın zamanlarda amatör matematikçilerin başarısız girişimleri olarak eğlence matematiğinin konusu haline gelen sözde dairesel kareler yayınlandı .

Özellikle matematiksel meslekten olmayanlar için yüksek çekiciliğinin ana nedenlerinden biri, muhtemelen, derinlemesine matematik bilgisi olmadan bile anlaşılabilen veya en azından anlaşılabilir görünen çok temel problemdir. Yerleşik bilim adamlarının sayısız başarısız çözüm girişimiyle birlikte, dairenin karesi gerçek bir nimbus elde etti .

Çemberin karesini almak için yapılan sayısız çabanın hafife alınmaması gereken bir başka nedeni de, sorunun çözümünün yüksek bir fiyata geleceğine dair yaygın kanaatti - muhtemelen daire karelemesinin doğrudan bağlantılı olduğu şeklindeki hatalı varsayıma kadar giden bir yanlış anlama. Uzun süredir çözülmemiş , denizde boylamın kesin olarak belirlenmesi sorunuyla , çözümü için aslında fiyatları ortaya çıktı. Yarışmanın destan bile 1891 böylece ısrarla devam Meyers Konversations-Lexikon olabilir hala "okuma Charles V teklif ettiğini 100.000 thalers ve Hollandalı Devletler Genel da yüksek toplamı".

Belirgin daire kareler

Çemberin karesini bulduğuna inanan amatör bir matematikçinin önde gelen örneği İngiliz filozof Thomas Hobbes'tur . 1665'te De corpore adlı çalışmasında yayınlanan çözümü - gerçekte bir yaklaşım inşası - aynı yıl John Wallis tarafından reddedildi. Takip eden dönemde, ikisi arasında Hobbes'un 1679'daki ölümüne kadar sona ermeyen keskin bir tartışma gelişti.

Lambert, belirli bir rasyonel değer aracılığıyla dairenin üç karesini bildirir. 18. yüzyılın ortalarında ortaya çıkan eserler, çapın eşit alan karesinin kenarına oranı için ³⁵ / ₃₁ yaklaşımına dayanmaktadır . Bu, daire sayısı için yaklaşık değeri verir.

${\ displaystyle \ pi \ yaklaşık {\ frac {3844} {1225}} = 3 {,} 1 {\ color {red} 37 \; 9 \; \ ldots} \ ;.}$

Üç yazardan biri, Ravensburglu vaiz Merkel , Gotthold Ephraim Lessing'in "Dairenin karesini almanın mucidi M ** üzerine" şiirini adadı .

Amerikalı doktor Edward J. Goodwin tarafından yapılan dairesel kareleme, 1894'te American Mathematical Monthly'nin ilk cildinde, sadece yazarın bir reklamı olarak bile ortaya çıktı . İşin kendisi kendisiyle çelişiyor ve okumaya bağlı olarak . Indiana Pi Bill olarak adlandırılan 1897 Indiana Parlamentosu tarafından sunulan bir yasa tasarısının temelini oluşturdu, Goodwin'in bulgularının yasaya dönüştürülmesi gerekiyor.${\ görüntü stili \ pi}$

Sanat ve Kültür

Bir sözde “daire squarer” veya “quadrator” görünümü en erken kanıt olarak, bir pasaj Aristofanes'in 'komedi Kuşlar 5. yy M.Ö. bazen edilir ki, anılan Meton görünen bir müfettiş ve zemin planının olarak geometrik araçlara sahip yeni bir şehir, “dairenin kareye dönüşmesini” tanımlamak ister. Bununla kastedilen, bir dairenin karelenmesi değil, ifade dairenin karesine bir gönderme gibi görünse bile, dik açılarda buluşan iki sokağın yaratılmasıdır.

1321 yılında Dante Alighieri, onun içinde İlahi Komedya, sunulan insan kavrayışının ötesinde bir görev olarak daireyi kareye ve Cenneti anlamak için kendi yetersizlik ile karşılaştırıldığında:

In James Joyce en çığır açan 1922 roman Ulysses , ana karakter Leopold Bloom , bir reklam edinen . 1882 yazında, sözde büyük bir servet elde etmek için dairenin karesini alma problemini çözmek için çok çalıştı . Romanın sonuna doğru, babası Rudolf Virág ile uzun bir diyalogda, ne yazık ki başarısız olduğunu kabul etmek zorunda kaldı.

Yaklaşık yapılar

Dürer'e göre Babil süreci (1525)

Bir pergel ve cetvel ile kesin bir çözüm mümkün olmasa da, daire kareleme için birçok amaç için yeterince kesin olan yaklaşık yapılar vardır. Antik çağda bilinen basit yöntemler, dairenin çapının veya yarıçapının karenin kenarına veya köşegenlerine tamsayı oranını gösterir. Rhind papirüsünde sözü edilen 9 çapındaki dairenin kenar uzunluğu 8 olan kare ile denklemine ek olarak, 8 çapındaki dairenin köşegenlerin 10 karesiyle olan denklemi de biliniyordu. Bu yapı bir yandan Babillilerde bulunurken, diğer yandan Romalı bilirkişi Vitruvius'un yayınlarında belirtilmiştir . Bu değer 3 ile döner ¹ / ₈ için . Albrecht Dürer , uygun bir çizim yöntemi sağlamak için 1525 yılında Vnderweysung der messung mit dem zirckel und richtscheyt adlı çalışmasında bu yapıyı yeniden ele almıştır . Tamamen yaklaşık bir çözüm olduğunun farkında olan Dürer, henüz kesin bir çözümün bulunmadığını açıkça yazıyor: ${\ görüntü stili \ pi}$

Kochański tarafından yapılan inşaat

Kochański (1685) tarafından yaklaşık yapım.

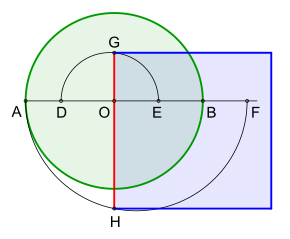
Çevrenin yarısı için klasik bir yaklaşık çözüm , 1685'te Polonyalı matematikçi Adam Adamandy Kochański tarafından keşfedildi. Sadece bir dairesel açıklığa ihtiyacı var. Gerçek yapı, yarım dairenin düzeltilmesinden oluşur. Kochanski, verilen yarıçaptan yaklaşık olarak düz bir uzunluk d çizgisi oluşturdu . H. dairenin çevresinin yaklaşık yarısı Sağdaki çizimde kırmızı ile çizilen dikdörtgen bu nedenle daire ile hemen hemen aynı alana sahiptir . Yaklaşık kareleme , dikdörtgenin karesinde açıklanan sağ üçgenin matematiksel yasalarının yardımıyla bu temelden çıkar . Kochański, daire numarasını dört ondalık basamağa yaklaştırıyor:${\ görüntü stili r}$${\ displaystyle r \ cdot \ pi,}$${\ görüntü stili {\ tfrac {U} {2}}.}$${\ displaystyle {\ overline {AZ}} \ cdot r = r \; \ cdot \ yaklaşık \ pi \ cdot r}$

${\ displaystyle \ pi = 3 {,} 141 \; 592 \ ldots \ yaklaşık {\ overline {AZ}} = r \ cdot {\ sqrt {(3- \ tan 30 ^ {\ circ}) ^ {2} + 4 \,}} \ \ yaklaşık \ 3 {,} 141 \; 5 {\ color {red} 33} \ cdot r}$

Hataları göstermek için örnekler:

Yarıçapı r = 100 m olan bir daire için kenar uzunluğunun hatası ≈ -1,7 mm olacaktır.

Yarıçapı r = 1 m olan bir daire için A alanının hatası ≈ −59 mm² olacaktır.

Jacob de Gelder tarafından inşaat

devamı (kesik çizgiler) ile Jacob de Gelder tarafından İnşaat.

1849'da, Jacob de Gelder'in (1765-1848) zarif ve açıkça basit bir yapısı Grünert'in arşivinde göründü . Bu, ZA Ramanujan'ın karşılaştırılabilir yapıyı yayınlamasından 64 yıl önceydi .

Yaklaşıma dayalıdır

${\ displaystyle \ pi \ yaklaşık {\ frac {355} {113}} = 3 {,} 141 \; 592 {\ color {red} \; 9 \; \ ldots}}$

ve değerin iki toplama bölünmesi

${\ displaystyle 3 + 0 {,} 141 \; 592 {\ color {red} \; 9 \; \ ldots}.}$

Bu kesrin değeri, daire numarasıyla zaten ortak olan altı ondalık basamağa sahiptir . 5. yüzyıldan Çinli matematikçi Zu Chongzhi'den gelir ve bu nedenle Zu Chongzhi kesri olarak da adlandırılır .${\ görüntü stili \ pi}$

Jacob de Gelder meydanın kenarını inşa etmedi; aşağıdaki değeri bulması onun için yeterliydi:

${\ displaystyle {\ overline {AH}} = {\ frac {4 ^ {2}} {7 ^ {2} + 8 ^ {2}}} = 0 {,} 141 \; 592 {\ color {red} \; 9 \; \ ldots}}$.

Bitişik resim - aşağıda açıklanan - Jacob de Gelder'in yapımını devamı ile göstermektedir.

Yarıçapı CD = 1 olan bir dairenin iki dik merkez çizgisi çizin ve A ve B kesişim noktalarını belirleyin . CE = mesafesini belirleyin ve E ile A'yı birleştirin. AE üzerinde ve A'dan AF = mesafesini belirleyin . Beraberlik FG paralel CD G ile ve bağlantı E çizin FH paralel EG , daha sonra AH = belirleyin BJ = CB ve ardından JK = AH . Yarıya AK L ve A L çevresinde Thales daire, kesişme noktası bu sonuçlar çekmek M. kademeli BM köküdür AK ve bu şekilde aranan, hemen hemen aynı kare yan uzunluğu. ${\ görüntü stili {\ tfrac {7} {8}}}$${\ görüntü stili {\ tfrac {1} {2}}}$${\ displaystyle {\ tfrac {4 ^ {2}} {7 ^ {2} + 8 ^ {2}}}.}$

Hataları göstermek için örnekler:

Yarıçapı r = 100 km olan bir daire için kenar uzunluğunun hatası ≈ 7,5 mm olacaktır.

Yarıçapı r = 1 m olan bir daire için A alanındaki hata ≈ 0,3 mm² olacaktır.

Tasarım EW Hobson

İnşaatın devamı ile birlikte EW Hobson'a göre yaklaşık inşaat.

1913'te EW Hobson tarafından özellikle basit ve kolay anlaşılır bir yapı yapılmıştır . Karenin kenarı için yalnızca üç yarım daire ve iki karşılıklı dik çizgi gerektirir .

Yandaki resim, aradığınız daire ve kare ile yapıyı göstermektedir.

Özellikler ve açıklama:

• Çaplı daire ${\ görüntü stili AOB}$
• ${\ displaystyle {\ overline {OD}} = {\ frac {3} {5}} \ cdot r, \; {\ overline {OF}} = {\ frac {3} {2}} \ cdot r, \ ; {\ overline {OE}} = {\ frac {1} {2}} \ cdot r.}$

Semicircles çizin ile ve çapı olarak. Son olarak, dik kurmak yoluyla oluşturulan kesişme noktaları tarafından bu ve temin yan uzunluğunu Aradığınız meydanda ${\ displaystyle DGE, AHF}$${\ displaystyle {\ üst çizgi {DE}}}$${\ displaystyle {\ üst çizgi {AF}}}$${\ görüntü stili {\ üst çizgi {AB}}}$${\ görüntü stili O.}$${\ görüntü stili G}$${\ görüntü stili H}$

${\ displaystyle {\ overline {GH}} = r \ cdot 1 {,} 772 \; 4 {\ color {red} 67 \ ldots} \; [LE].}$

Yarıçapı olan bir daire için , karenin kenarındaki dört ondalık basamak aşağıdakilerle aynıdır.${\ görüntü stili r = 1 \; [LE]}$${\ displaystyle {\ sqrt {\ pi}} = 1 {,} 772 \; 453}$

Hataları göstermek için örnek:

Yarıçapı r = 100 m olan bir daire için kenar uzunluğunun hatası ≈ 1.4 mm olacaktır.

Yarıçapı r = 1 m olan bir daire için A alanının hatası ≈ 46 mm² olacaktır.

SA Ramanujan tarafından yapılan inşaatlar

SA Ramanujan'a (1913) göre yaklaşık yapı, çizilmiş kare ile

Ayrıca 1913'te Hintli matematikçi Srinivasa Ramanujan tarafından yine yaklaşıklığa dayalı bir yapı ortaya çıktı.

${\ displaystyle \ pi \ yaklaşık {\ frac {355} {113}} = 3 {,} 141 \; 592 {\ color {red} \; 9 \; \ ldots}}$

dayanır. Ramanujan, yönteminin doğruluğu ile ilgili olarak, 140.000 mil karelik dairesel bir alanla, karenin inşa edilmiş tarafının gerçek değerden sadece yaklaşık bir inç saptığını kaydetti.

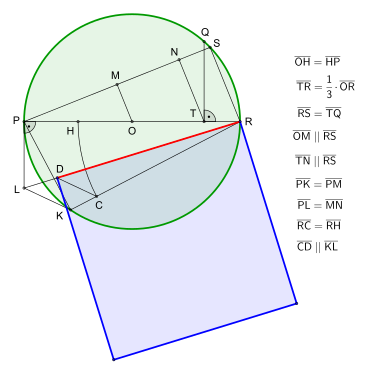
Açıklama (çeviri):

PQR, O merkezli ve PR'nin çapı olan bir daire olsun. PO'yu H'de yarılayın ve T, OR'nin R yakınında üçlü bölümünden nokta olsun. TQ'yu PR'ye dik çizin ve kirişi RS = TQ olarak ayarlayın.

P'yi S ile bağlayın ve OM ve TN'yi RS'ye paralel çizin. Bir kiriş PK = PM ayarlayın ve PL = MN tanjantını çizin. R ile L, R ile K ve K ile L ile bağlayın. Bölüm RC = RH. CD'yi KL'ye paralel çizin, [CD] D'de RL ile buluşur.

O zaman RD üzerindeki kare yaklaşık olarak PQR dairesine eşittir.

Çünkü ${\ displaystyle RS ^ {2} = {\ frac {5} {36}} d ^ {2},}$

dairenin çapı nerede .${\ görüntü stili d}$

sonuç olarak ${\ displaystyle PS ^ {2} = {\ frac {31} {36}} d ^ {2}.}$

Ama ve aynı veya${\ görüntü stili PL}$${\ görüntü stili PK}$ ${\ görüntü stili MN}$ ${\ görüntü stili PM.}$

Böylece ve${\ displaystyle PK ^ {2} = {\ frac {31} {144}} d ^ {2},}$ ${\ displaystyle PL ^ {2} = {\ frac {31} {324}} d ^ {2}.}$

sonuç olarak ${\ displaystyle RK ^ {2} = PR ^ {2} -PK ^ {2} = {\ frac {113} {144}} d ^ {2},}$

ve ${\ displaystyle RL ^ {2} = PR ^ {2} + PL ^ {2} = {\ frac {355} {324}} d ^ {2}.}$

ancak ${\ displaystyle {\ frac {RK} {RL}} = {\ frac {RC} {RD}} = {\ frac {3} {2}} {\ sqrt {\ frac {113} {355}}}, }$

ve ${\ displaystyle RC = {\ frac {3} {4}} d.}$

Yani neredeyse aynı.${\ displaystyle RD = {\ frac {d} {2}} {\ sqrt {\ frac {355} {113}}} = r {\ sqrt {\ pi}},}$

Not: Dairenin alanı 140.000 mil kare ise, RD gerçek uzunluğundan yaklaşık bir inç daha büyüktür.

SA Ramanujan'a (1914) göre yaklaşık yapı, yapının devamı ile (kesik çizgiler), animasyona
bakın .

Ertesi yıl (1914) bir çalışmasında, Ramanujan, diğer yaklaşım yöntemlerine ek olarak, bir pergel ve cetvelle başka bir kare alma sağladı. Bu değer yatıyor

${\ displaystyle \ pi \ yaklaşık {\ sqrt [{4}] {9 ^ {2} + {\ frac {19 ^ {2}} {22}}}} = 3 {,} 141 \; 592 \; 65 {\ color {kırmızı} 2 \; \ ldots}}$

ki bu bile sekiz basamağa yaklaşıyor. Bu karelemede Ramanujan, aradığı karenin kenar uzunluğunu oluşturmadı; OS rotasını göstermesi onun için yeterliydi. Sağdaki yapının devamında, OS segmenti, OB segmenti ile birlikte ortalama orantılı (kırmızı segment OE) temsil etmek için kullanılır . ${\ görüntü stili \ pi}$

Açıklama (çeviri):

AB (Şekil 2) merkezi O olan bir dairenin çapı olsun. Dairesel ark ACB'yi C'de ve üçüncü AO'yu T'de yarıya bölün. B'yi C ile bağlayın ve AT ile aynı uzunlukta CM ve MN'yi işaretleyin. A'yı M'ye ve A'yı N'ye bağlayın ve AP'yi AM olarak işaretleyin. Q'nun AM ile buluştuğu yerde PQ'yu MN'ye paralel çizin. O'yu Q ile bağlayın ve TR'yi R'nin AQ ile buluştuğu OQ'ya paralel çizin. AO ve Ap ile aynı uzunlukta, daha sonra S ile bağlantı O AS dik çizmek ortalama orantılı hatası daha az onikinci olmak üzere çok yakın çevresinin bir altıncı olacak OS ve OB arasındaki inç halinde çap 8000 Mil uzunluğundadır.

İstenen kenar uzunluğuna yapı kadar sürdürülmesi kare: uzatmak AB A ötesinde burada b dairesel ark tutuşturmak ₁ yarıçapı ile bunun etrafında OS 'S, bu sonuçlar. Yarıya BS ' D ve b, Thales daire çizin ₂ b Thales daire C ile O arasından düz bir çizgi D boyunca ₂ , bu b kesişen ₂ E. OE segmenti olup olarak da adlandırılır OS ve OB arasındaki ortalama orantılı Yukarıda tanımlanan geometrik ortalama , Öklid'in yükseklik teoreminden kaynaklanır. Mesafesi uzatma EO O ötesine ve daha sonra aktarma EO , iki kez daha, F ve A bu sonuçlar ₁ ve böylece mesafe uzunluğu EA ₁ yaklaşık değerde yarı çap , yukarıda tarif edilen . EA ₁ doğrusunu G'de yarıya bölün ve Thales dairesini b ₃ G üzerinde çizin. OB doğrusunu A _1'den EA ₁ doğrusuna aktarın , bu H ile sonuçlanır. EA ₁ üzerinde H'den Thales dairesi b _3'e dikey bir doğru oluşturun , kendisi sonuçlanıyor B ₁ . A _1'i B _1'e bağlayın , böylece aradığınız kenar uzunluğu neredeyse eşit bir A ₁ B ₁ C ₁ D ₁ karesi için oluşturulur . ${\ görüntü stili a}$
${\ görüntü stili \ pi}$${\ görüntü stili a}$

Hataları göstermek için örnekler:

Yarıçapı r = 10.000 km olan bir daire için kenar uzunluğunun hatası ≈ -2,8 mm olacaktır.

Yarıçapı r = 10 m olan bir daire için hata A ≈ −0,2 mm² alanı olacaktır.

Louis Loynes tarafından inşaat

Loynes'in yapımı (1961).

Bu alan bulgusuna dayanmaktadır Louis Loynes 1961 yayınlanan basit bir yöntem çevresi bir dik üçgen daha kareye eşit dik kenar zaman olduğu teğet daha dik kenar daha küçük oranı küçük bir açı bölgesinin olduğu

${\ displaystyle {\ sqrt {{\ frac {4} {\ pi}} - 1}} = 0 {,} 5227232 \ nokta}$

kesre çok yakın bir değerdir

${\ displaystyle {\ frac {23} {44}} = 0 {,} 5227272 \ nokta}$

yalanlar. Bu, kareye 23:44 katetus oranıyla (yapılandırılabilir) dik açılı üçgeni kullanarak basit bir yaklaşımla sonuçlanır. Daire sayısı için yaklaşık değer

${\ displaystyle \ pi \ yaklaşık {\ frac {7744} {2465}} = 3 {,} 141 \; 5 {\ color {red} 82 \; \ ldots}}$

Kochański'nin yapısından biraz daha iyidir.

Hataları göstermek için örnekler:

Yarıçapı r = 1 km olan bir daire için kenar uzunluğunun hatası ≈ -3 mm olacaktır.

Yarıçapı r = 1 m olan bir daire için A alanının hatası ≈ −11 mm² olacaktır.

İnşa edilmiş bir kesir kullanarak yaklaşık çözüm

Değeri yaklaşık olarak daire sayısına tekabül eden bir ışın üzerine bir kesir oluşturulursa, üçüncü ışın teoremi yardımıyla, istenen sayıda ondalık basamağı temsil etmek az ya da çok yapıcı bir çaba ile mümkündür . Kare kutunun kenar uzunluğunu belirlemek için. B. mola ${\ görüntü stili \ pi}$ ${\ görüntü stili \ pi}$

${\ displaystyle {\ frac {245850922} {78256779}} = 3 {,} 141 \; 592 \; 653 \; 589 \; 793 {\ color {red} \; 160 \; \ ldots}}$

kullanılabilir. Daire sayısının bir tahmini olarak, etkileyici bir on beş eşit ondalık basamak sağlar. Tersine dönmesi bu kısmından gelmektedir Johann Heinrich Lambert adlı kitabında bunu yayınlanmış, Matematik ve Uygulamaları Kullanımına tarihinden gibi erken 1770 olarak . ${\ görüntü stili \ pi}$

Kare indeksler kullanan klasik olmayan yöntem

Pergel ve cetvel kısıtlamasını gevşetirseniz ve daha fazla inşaat aracına izin verirseniz, dairenin karesini almak veya karenin kenar uzunluğunu tam olarak oluşturmak için çok sayıda olasılık elde edersiniz . ${\ görüntü stili {\ sqrt {\ pi}}}$

Özel aşkın eğrilerin yardımıyla, sözde kuadratris , tek ek araç olarak, bir daireyi tam olarak kare yapmak mümkündür. Böyle bir kare matrisin varlığı veya mevcudiyeti, matematiksel modelde basitçe varsayılır. Kağıt üzerinde pratik çizim için, örneğin bir şablon veya bir çizici çıktısı şeklinde mevcuttur ve ayrıca bu tür eğrilerin oluşturulabileceği bazı özel mekanik çizim cihazları da vardır. Antik çağlardan beri bilinen ve dairesel kareleme için kullanılan en eski kuadratriler z'yi içerir. B. Hippias'ın Quadratrix'i ve Arşimet'in spirali aşağıda açıklanan eğriler .

Hippias'ın dörtgenini kullanarak dairenin karesini alma

Şekil 1 Hippias ait quadrix, yardımıyla bir daire kareleme Grafik, bu çalışan içinden ve .${\ displaystyle E, \; {\ tfrac {2} {\ pi}}}$${\ görüntü stili D}$

Daire sayıda inşaat sonra birlikte ilave bir yardım olarak Hippias en quadratrix , mesafe uzatarak göre Thales teoremi, kök sonuçlar gelen kenar uzunluğu ile çizilen kare daire etrafında tam olarak aynı alana sahip${\ görüntü stili \ pi}$${\ görüntü stili {\ üst çizgi {BH}}}$${\ displaystyle {\ üst çizgi {A \ pi}} = {\ üst çizgi {AI}} = {\ sqrt {\ pi}}.}$${\ görüntü stili {\ sqrt {\ pi}}}$${\ görüntü stili A.}$

• 

  Şekil 1
  Ek bir yardım olarak Hippias'ın dörtgeni ile dairenin karesini alma.

• 

  Şekil 2
  Ek bir yardım olarak Arşimet spirali ile dairenin karesini alma.

Arşimet spiralini kullanarak dairenin karesini alma

Şekil 2, bir dairenin nispeten basit bir karesini göstermektedir. Ek bir yardımcı olarak bir Arşimet spirali kullanıyor . Dönme açısı spiral edilir o şekilde seçilmelidir sonuçlanır. Spiralin grafiği ekseni keser ve seçilen dönüş açısı nedeniyle daire sayısını bir segment olarak verir .${\ görüntü stili \ varphi}$${\ görüntü stili a = 2}$${\ displaystyle 2 \ cdot {\ tfrac {\ pi} {2}} = \ pi}$${\ görüntü stili y}$${\ görüntü stili B}$${\ displaystyle \ varphi = \ pi}$${\ displaystyle {\ overline {OB}}.}$

Şimdi yapmanız gereken tek şey eksene daire sayısını yansıtmak ve kökü oluşturmak.Son olarak çizilen ve kenar uzunluğu olan kare, etrafındaki daire ile tam olarak aynı alana sahip.${\ görüntü stili \ pi}$${\ görüntü stili x}$ ${\ görüntü stili {\ sqrt {\ pi}}.}$${\ görüntü stili {\ sqrt {\ pi}}}$${\ görüntü stili O.}$

varyantlar

Tarski'nin dairenin karesini alma problemi

1925'te Alfred Tarski , bir daireyi herhangi bir sayıda parçaya bölme ve daha sonra onları saf hareketle (yani esnetmeden) hareket ettirme görevini belirledi, böylece bir kare elde edildi.

Miklós Laczkovich 1989'da bir çözüm buldu: Bir daireyi sonlu sayıda parçaya bölmenin ve onları sadece hareketle hareket ettirerek bir kare oluşturmanın mümkün olduğunu kanıtladı . Daireyi 10 ⁵⁰ parçaya böldü. Bununla birlikte, ispat için, bugün çoğu bilim adamı tarafından kabul edilen, ancak elbette bir mesele olmayan seçim aksiyomuna ihtiyacı var . Kanıt Banach-Tarski paradoksuna çok benzer .

Laczkovich, (seçim aksiyomunu varsayarak) böyle bir ayrıştırmanın var olduğunu kanıtlamıştır, ancak bu ayrıştırma açıkça ifade edilemez.

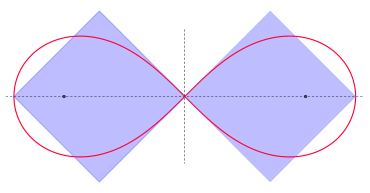
Lemniscates

Lemniscate'in karesini alma.

Dairenin aksine , aynı alanı kapsayan bir lemniscate (∞) için iki kare oluşturmak mümkündür . Kenar uzunlukları en büyük lemniskat yarıçapına a karşılık gelir  .

Ayrıca bakınız

• Dikdörtgenin karesini alma
• karenin karesini almak
• Çokgeni dörtgen haline getir

Literatür ve kaynaklar

Genel olarak

• Eugen Beutel: Çemberin karesini alma . 2. Baskı. Teubner, Leipzig 1920. (sayısallaştırılmış versiyon)
• Moritz Cantor : Matematik tarihi üzerine dersler. Teubner, Leipzig 1880-1908, 4 cilt. (Dijitalleştirilmiş versiyon)
• Helmuth Gericke : Antik Çağ ve Doğu'da Matematik. Springer, Berlin 1984, ISBN 3-540-11647-8 .
• Helmuth Gericke: Batı'da Matematik. Springer, Berlin 1990, ISBN 3-540-51206-3 .
• Thomas Little Heath: Yunan Matematiğinin Tarihi . Cilt 1. Clarendon Press, Oxford 1921. (Dover, New York 1981, ISBN 0-486-24073-8'de yeniden basılmıştır .)
• Klaus Mainzer: Geometri Tarihi. Bibliographisches Institut, Mannheim ve ark. 1980, ISBN 3-411-01575-6 .
• Ferdinand Rudio : Arşimet, Huygens, Lambert, Legendre. Dairesel ölçüm üzerine dört risale. Teubner, Leipzig 1892. (sayısallaştırılmış versiyon)

aşkınlığına ${\ görüntü stili \ pi}$

• Ferdinand Lindemann: Sayı hakkında . ${\ görüntü stili \ pi}$İçinde: Mathematische Annalen , 20, 1882, s. 213–225 ( dijitalleştirilmiş versiyon ).
• David Hilbert: e ve sayılarının aşkınlığı hakkında . ${\ görüntü stili \ pi}$İçinde: Mathematische Annalen , 43, 1893, s. 216-219 ( dijitalleştirilmiş versiyon ).
• Lorenz Milla: Çemberin aşkınlığı ve çemberin karesi${\ görüntü stili \ pi}$ . 2020, arxiv : 2003.14035
• Paul Albert Gordan: e ve . ${\ görüntü stili \ pi}$İçinde: Mathematische Annalen , 43, 1893, s. 222-224 ( sayısallaştırılmış versiyon ).
• Theodor Vahlen: Lindemann'ın üstel fonksiyonla ilgili teoreminin kanıtı. İçinde: Mathematische Annalen , 53, 1900, s. 457-460 ( sayısallaştırılmış versiyon ).

eğlence matematik

• Underwood Dudley: Delilik ve Şaka Arasındaki Matematik. Yanılgılar, Yanlış Kanıtlar ve 57 Sayısının Amerikan Tarihindeki Önemi . Birkhäuser , Basel 1995, ISBN 3-7643-5145-4 (İngilizce orijinal başlık: Matematiksel kranklar ).

İnternet linkleri

Vikisözlük: Dairenin karesini alma  - anlam açıklamaları, kelime kökenleri, eş anlamlılar, çeviriler

... 245850922 78256779 ile Johann Heinrich Lambert'ten bir kesrin tersi ${\ görüntü stili:}$

• Dairenin karesini alma - MacTutor Matematik Tarihi arşivi (İngilizce)

Bireysel kanıt