açıyı üçe böl

Sorun ve trisectioning açısı (aynı zamanda: açı triseksiyon ) anlaşılır olarak geometri rasgele sorusuna açısı üç eşit ayrılabilir açıları pergel ve (ile cetvel yardımıyla Öklid araçlar ). Açının üçlü bölümü, antik matematiğin üç klasik probleminden biridir ve sadece belirli açılar için gerçekleştirilebilir. Açıları üçe bölme sorunu antik çağa kadar dayansa da cebir yöntemlerinin genellikle pusula ve cetvelle çözülemeyeceğini göstermek için kullanılması 19. yüzyıla kadar sürmüştür . Bu olumsuz ifadenin ilk kanıtı 1837 yılından Pierre Wantzel'den gelir. Onda problem üçüncü dereceden bir cebirsel denkleme indirgenir ve çözümlerinin sonlu sayıda adımda oluşturulabilecek sayılar olmadığını iddia eder. Sadece yapının genel olarak çalışmadığının gösterilmesi gerektiği için tek bir karşı örnek vermek yeterlidir. Örneğin pergel ve cetvelle 20° açı oluşturulamaz, bu nedenle 60° açı bu araçlarla üçe bölünemez.

Klasik bir yapı mümkün olmasa da, bir açının üçe bölünmesi, işaretli bir cetvel gibi yardımcı malzemeler yardımıyla hassas bir şekilde gerçekleştirilebilir. Bu tekniklerin bazıları eski zamanlarda zaten biliniyordu. Açıyı üç parçaya bölme problemine çarpıcı bir tezat olarak, açıortay kullanarak açıyı bir pergel ve cetvelle ikiye bölmenin çok kolay bir yolu vardır.

Klasik sorun

Klasik kurala göre, bir çözüm ancak herhangi bir açının bir pusula ve ölçeksiz bir cetvel yardımıyla üç eşit parçaya bölünmesi durumunda geçerlidir.

Özel açılarla, açıyı üçe bölmek mümkündür, örneğin her tamsayı 9 ° 'nin katları ile.

Eski Yunanlılar bile herhangi bir açı için genel bir çözüm bulmaya çalıştılar. 1830 civarında, Fransız matematikçi Évariste Galois , bunun genellikle mümkün olmadığına dair daha sonraki kanıtların temellerini attı . Örneğin, 20 ° oluşturulamadığından, 60 ° oluşturulabilir açıyı üçe bölmek mümkün değildir.

Bunun neden imkansız olduğu , İmkansızlığın İspatı bölümünde açıklanmıştır .

Bu nedenle, genel bir üç yollu bölme, nihai olarak, yalnızca pergel ve cetvellere ek olarak - trisektris gibi - ek yardımlar kullanılırsa veya cetvel üzerinde işaretler yapılırsa mümkündür. Öte yandan, aşağıdaki örneklerin gösterdiği gibi, herhangi bir iyi yaklaşım çözümü bir pusula ve cetvelle gösterilebilir.

Öykü

antik çağ

Öyleydi Yunanlılar kim MÖ 5. yy'da BC, keyfi bir açıyı üç eşit açıya bölme sorununu kabul etti. Muhtemelen bu problem, astronomik amaçlar için bir akor tablosu oluşturmaya çalıştıklarında matematiksel ilginin önüne geçmiştir . Pusulalar ve işaretsiz bir cetvelle ustalaşılabilecek bir çözüm için çabaladılar - Sakız Adası Oinopides'e (~ 440 M.Ö.) kadar uzanan bir sınırlama - ama bu gereksinimi karşılayan herhangi bir çözüm bulamadılar. Örneğin, ile tendon Batlamyus tablosu birinin temel geometrik artık yönetilebilir bir görev karşılaşır kazanıyor için tendonu için tendon . Nicolaus Copernicus'a (1473-1543) kadar yüzyıllar boyunca , tendonların geometrisi için gerekli olan trigonometri , sadece astronominin bir bileşeni olarak anlaşılmış ve buna göre astronomik çalışmalarda ele alınmıştır. Regiomontanus , trigonometri üzerine ilk bağımsız ders kitabını 1464 civarında yazdı , ancak bu kitap ancak ölümünden yaklaşık 70 yıl sonra, 1533'te yayınlandı.${\ displaystyle 3 ^ {\ circ}}$${\ displaystyle 1 ^ {\ circ}}$

Elis'li Hippias ( MÖ 460-400 civarı) MÖ 422 civarında ilk bulan kişiydi. Sözde ek yardım yardımıyla bir çözüm. Yardımcı bir eğriydi , Trisektrix des Hippias veya Quadratrix des Hippias olarak bilinmeye başladı . Bu, bir açıyı eşit parçalara bölmek için bile tasarlanmıştır . Quadratrix adı, dairesel kareleme sorununa da cevap verdiği gerçeğinden gelir . Buradan bunun aşkın bir eğri olduğu sonucuna varılabilir . Bununla birlikte, iki basit hareketle oluşturulduğu için üzerine yazmak kolaydır.${\ görüntü stili n}$

Syracuse Arşimet (MÖ 287-212) pragmatik bir çözüm buldu. Arşimet'e atama yapılmamış olsa da, sadece Arapça olarak hayatta kalan düzenli yedigenin bir yapısı vardır. Düzenli üçgenler, kareler, beşgenler ve altıgenler, verilen bir daire içinde bir pusula ve cetvel ile tanımlanabilirken, bu artık yedigen ile mümkün değildir. Cebirsel olarak, daireyi yedi eşit parçaya bölmek kübik bir denkleme yol açar ve bu nedenle küpü ikiye katlamak ve açıları üçe bölmekle aynı problem sınıfına aittir . Arşimet'in bulduğu iddia edilen yapı sadece bu iki aletle çalışır, ancak cetveli Öklid geometrisinde izin verilmeyen bir şekilde kullanır: İki üçgene kadar sabit bir nokta etrafında döndürülür, bunlardan biri dönüş arttıkça büyürken, diğeri azalıyor, alanda eşit. Bu, kaydırılabilir yapının özel bir türüdür veya Neusis olarak adlandırılır. Kullanılan yöntem teorik olarak ilgi çekici olsa da pratikte kullanılamamaktadır. Bugün Neusis inşaatı olarak adlandırılıyor . Arşimet daha sonra spiral ( Arşimet spirali ) olarak adlandırılan özel bir eğri yarattı ve bunu dairenin açısal bölümünü ve karesini incelemek için kullandı.

MÖ 2. yüzyılda MÖ Nicomedes icat mümkün mekanik Pappos tarafından verildiğine Neusis inşaat taleplerini karşılamak üzere yapılan bir enstrüman. Bununla oluşturulabilen eğrilere, şekillerinden dolayı İngilizce kabuk eğrilerinde conchoid adı verildi . Enstrüman, üçüncü birinin üzerinde belirli bir şekilde hareket edebildiği, birbirine sıkıca bağlı iki T-şekilli cetvelden oluşur. Böylece açıyı üçe bölmek için ek bir yardımcı olarak hizmet etti.

İskenderiyeli Pappos ( MS 4. yüzyılda) İskenderiye Neoplatonistlerinin çevresine aitti . Onun koleksiyonları sekiz kitap bir derlemesi olan; birincisi ve ikincisinin başlangıcı hariç hepsi korunmuştur. Erken modern dönemde, Avrupalı ​​matematikçiler , Öklid , Apollonios , Arşimet ve diğer matematikçilerin yazılarından önemli alıntılar içerdikleri için Koleksiyonlardan birçok öneri aldılar . Pappos, bu alıntıları eleştirel yorumlar ve kendi eklemelerinden bazılarıyla genişletti. Diğerlerinin yanı sıra gösterdi. cihazlarıyla açısal trisection çözümü için iki farklı varyant - ilave bir yardım, yani Neusis yapı (Bakınız olarak belirgin bir cetvelle pragmatik bir Pappos yöntemi ) ve kullandığı bir ikinci bir trisectrix olarak hiperbol .

Erken Orta Çağ

Ahmed ibn Mūsā, 9. yüzyılın ortalarında Bağdat'ta yaşamış ve kendilerine Banu Mūsā adını veren üç kardeşten biridir . O bir astronom ve matematikçiydi. Çözümü, belirli bir noktadan geçen bir hiperbolün önceden belirlenmiş iki asimptotunu gösterir . Açıyı üçe bölmek için işaretli bir cetvel ve dolayısıyla bir Neusis yapısı gereklidir. Onun çözümü Pappos'un kağıt şerit yapısına çok benziyordu (bkz . Pappos Metodu ).

Bağdatlı Sabit ibn Kurra (826-901) başlangıçta bir sarraftı, bilime ilgi duydu, matematik eğitimi aldı ve ayrıca felsefe ve astronomi okudu. Ayrıca Neusis inşası için hiperbol kullandı. Ahmed ibn Mûsâ'nın aksine, inşası daha kesin olarak tarif edilmiş ve daha ayrıntılı olarak gerekçelendirilmiştir. Çözümü de Pappo'nun kağıt şerit yapısına çok benziyordu.

Müslüman astronomi ve trigonometri de 15. yüzyılda doruğa ulaştı Uluğ Bey rasathane içinde Semerkant'ta . Orada El-Kaşi'nin yetenekli bir aktif, yineleme sinüs açısı üçlü denklemden büyük bir hassasiyetle için yararlandığı hesapla. Prensip olarak, aşağıdaki gibi devam etti. Bu yana gerekli olduğunca mükemmel bir şekilde tespit edilebilir (örneğin, bu arasındaki farktan inşa edilebilir beşgen ve pusula ve cetvelle altıgen), o kullanılan denklem üç bölme açıları ${\ displaystyle 1 ^ {\ circ}}$${\ displaystyle \ günah (3 ^ {\ circ})}$${\ displaystyle 36 ^ {\ circ}}$${\ displaystyle 30 ^ {\ circ}}$

${\ displaystyle \ sin (3 \ alpha) = 3 \ sin (\ alpha) -4 \ sin (\ alpha) ^ {3}}$.

İlk olarak bu trigonometrik gösterimde 16. yüzyılın sonunda Vieta'da bulundu . O tiptir (önceki sınıflandırmada katsayılar vardı - burada , - pozitif olduğu varsayılır). Al-Kashi gelen ilk yaklaşımının bilgisayarlı için . İkinci yaklaşım daha sonra benzer şekilde vb.'den gelir , burada özel bir özellik, her adımda tam olarak bir altmışlık noktanın tam olarak belirlenebilmesidir. Ondalık gösterime dönüştürülen al-Kashi'nin sonucu 18 basamak sağlar:${\ displaystyle x ^ {3} + q = piksel}$${\ görüntü stili p = {\ tfrac {3} {4}}}$${\ displaystyle q = {\ tfrac {1} {4}} \ günah (3 ^ {\ circ})}$${\ displaystyle x = {\ tfrac {q + x ^ {3}} {p}} \ yaklaşık {\ tfrac {q} {p}}}$${\ displaystyle x_ {1} = {\ tfrac {q} {p}}}$${\ displaystyle x_ {2} = {\ tfrac {q + x_ {1} ^ {3}} {p}}}$

${\ displaystyle \ günah (1 ^ {\ circ}) = 0 {,} \, 017 \, 452 \, 406 \, 437 \, 283 \, 571 \, \ nokta}$

Doğu kütüphanelerinde çok sayıda Arapça el yazması hala görülmemektedir, bu nedenle araştırmalar henüz gelişmenin ve elde edilen bilginin tam bir resmini çıkaramamıştır.

Modern zamanlara Rönesans

Bir matematikçi olarak Albrecht Dürer , üç boyutlu açılar bölümü teorisine de katkıda bulundu. Normal 7-, 9-, 11- ve 13-köşe için iyi yaklaşım yapılarına ek olarak, Underweysung'un ikinci kitabı da yaklaşık üç yollu bölümü içerir. 1931'de aynı problemin diğer birkaç yaklaşık çözümü ile karşılaştırıldı ve kesin değerden hiçbir yerde yaklaşık 20 ark saniyeden fazla sapmadığı ve böylece önerilen tüm diğer çözümleri geride bıraktığı gösterildi . Dürer'in tasarım fikri de kolayca yinelenebilir ve birkaç adımdan sonra çok yüksek düzeyde doğruluk sağlar. Her şeyde, Dürer her zaman kesin arasındaki temel farkın farkındadır, bunları ispatlayıcı olarak adlandırır ve yaklaşık çözümler, mekanik olarak adlandırır ve bu nedenle zamanının profesyonel matematikçilerinin çoğundan bile sıyrılır.

Pergel ve cetvel sadece bir çift kullanarak - - ilk insan sorunu çözülemez olduğunu kanıtlamak oldu Pierre-Laurent Wantzel Ancak tarihçiler Wantzel ilk kişi oldu şüphe 1837 yılında biliyor kanıtı genç olarak, Carl Friedrich Gauss yaptığı çok muhtemelen bir tane vardı. 1801'de yayınlanan Disquisitiones aritmeticae adlı çalışmasının büyük bir kısmı, bir polinom denkleminin kare radikallerle çözülebilmesi için hangi koşulları karşılaması gerektiği sorusuna ayrılmıştır . Orada ayrıca, Gauss'un adını taşıyan, çoğu klasik görevin çözümsüzlüğünün bir pusula ve cetvelle gösterilebildiği cümleleri de bulacaksınız. Gauss geliştirdiği tekniklerle örneğin 17 kenarlının pergel ve cetvelle yapılabileceğini kanıtladı . Matematik tarihçileri Christoph Scriba ve Peter Schreiber , Wantzel'in yine de birçok yazar tarafından cümlelerin yaratıcısı olarak adlandırılması ve alıntılanması gerçeğini , 19. yüzyılda bilimin "iletişim güçlüklerine" bağlar .

imkansızlığın kanıtı

Kanıt tarihi

Pierre Wantzel 1837'de bir kareyi pergel ve cetvelle üç eşit parçaya bölmenin genellikle imkansız olduğuna dair bir kanıt yayınladı . Kanıtı, eğer modern terminolojide ifade edilirse , soyut cebirde ve özellikle Galois teorisinde ele alınan alan uzantılarını kullanır . Wantzel, bu sonuçları Galois'ten (çalışması 1846'da çıkan) daha önce yayınladı ve vücut uzantıları ile Galois teorisinin ilgilendiği gruplar arasındaki bağlantıya ihtiyaç duymadı . Onun kanıtı aşağıdaki cebirsel düşüncelere dayanıyordu:

1. İspatın ilk bölümünde, eğer bir tasarım problemi bir cetvel ve pergel ile çözülebiliyorsa, “sorunun bilinmeyeni, katsayıları parametrelerin rasyonel fonksiyonları olan bir dizi ikinci dereceden denklemi çözerek elde edilebileceğini savunuyor. bir sorunu ve The kökleri önceki denklemlerin “dir.${\ displaystyle p, q, r, \ noktalar}$

"Sorun bilinmiyor", örneğin aradığınız rota anlamına gelir .${\ displaystyle x = \ cos (\ alpha)}$

2. Daha sonra her cebirsel sayının bir sistemin son denkleminin çözümü olduğunu gösterdi.${\ displaystyle x_ {n} ^ {0}}$${\ displaystyle x_ {n} ^ {2} + A_ {n-1} x_ {n} + B_ {n-1} = 0}$

${\ displaystyle {\ start {hizalı} & x_ {1} ^ {2} + Ax_ {1} + B = 0 \\ & x_ {2} ^ {2} + A_ {1} x_ {2} + B_ { 1} = 0 \\ & \ vdots \\ & x_ {n} ^ {2} + A_ {n-1} x_ {n} + B_ {n-1} = 0 \ bitiş {hizalanmış}}}$

katsayılarını, olduğu zaman içinde vücut birbirini takip eden birleşim , çözer derece polinom denklemi katsayılı . Bunu yapmak denklemi çözer ve sorunun verilen parametreleridir.${\ displaystyle A_ {m}, B_ {m}}$ ${\ displaystyle \ mathbb {Q} (p, q, r, \ dots, x_ {1} ^ {0}, \ dots, x_ {m} ^ {0})}$${\ displaystyle 2 ^ {n}}$${\ displaystyle \ mathbb {Q} (p, q, r, \ noktalar)}$${\ displaystyle x_ {j} ^ {0}}$${\ displaystyle x_ {j} ^ {2} + A_ {j-1} x_ {j} + B_ {j-1} = 0}$${\ displaystyle p, q, r, \ noktalar}$

3. Wantzel, yeterince büyük olarak seçilirse, her cebirsel sayının, kuvveti iki olan bir polinomun sıfırı olduğunu biliyordu. Dolayısıyla, ana sonuç gerekli denklemlerin sayısı minimuma düşürülmesi halinde, ortaya çıkan polinom olduğunu göstermekti indirgenemez üzerinde .${\ displaystyle \ mathbb {Q} (p, q, r, \ noktalar)}$

Şimdi , 1'den 3'e kadar olan cümlelerin bir sonucu olarak, yapının imkansızlığı aşağıdaki gibidir : 0, 1 ve 'den başlayarak, bir açıyı bir pergel ve cetvelle üçe bölmek mümkün olsaydı, o zaman indirgenemez bir polinomun sıfırı olurdu. yukarıda olmalı , derece iki Has'ın bir gücü olmalıdır . Polinom olduğu genel indirgenemez fazla , ancak bu bir çelişki derecesi 3 sahiptir. ${\ displaystyle \ çünkü (3 \ alfa)}$${\ görüntü stili 3 \ alfa}$${\ displaystyle \ cos (\ alpha)}$${\ displaystyle \ mathbb {Q} (\ cos (3 \ alpha))}$${\ displaystyle 4x ^ {3} -3x- \ cos (3 \ alfa)}$${\ displaystyle \ mathbb {Q} (\ cos (3 \ alpha))}$

Wantzel'in orijinal yayınının matematikçi Jesper Lützen tarafından eksik ve anlaşılması zor olarak görüldüğüne dikkat edilmelidir - bu her şeyden önce ana önerme 3'ün “kanıtı” için geçerlidir. modern teknik dil. Wantzel'in açının üçlü bölünmesini ve küpün bir cetvel ve pergel ile ikiye katlanmasını oluşturmanın imkansızlığına dair kanıtı, 1837'de yayınlanmasından sonra neredeyse bir yüzyıl boyunca unutuldu. Lützen'e göre, "yazarın kötü şöhretli olmaması", "çağdaşlarından bazılarının sonucu bilinen, hatta ispatlanmış sayması" ve "sonucun yazıldığı dönemde önemli bir matematiksel sonuç olarak görülmemesidir. yayın” sürüş nedenleri.

cebirsel kanıt

Belirli bir boyutta bir açı oluşturma sorunu , uzunlukları birbiriyle ilişkili iki doğru oluşturmaya eşdeğerdir . Bu iki problemden birinin pergel ve cetvel ile çözümü diğerinin çözümü ile sonuçlanır. Üç açılı kosinüs formülünü kullanma${\ görüntü stili \ alfa}$${\ displaystyle \ cos (\ alpha)}$

${\ displaystyle \ cos (3 \ alpha) = 4 \ cos ^ {3} (\ alpha) -3 \ cos (\ alpha)}$

Bir cebirsel denklem değerlerini bağlayan kurulabilir ve . Açısal üçe bölme problemi, hat uzunluğunun birim uzunluğa oranının belirli bir kübik denklemin çözümüne eşit olduğu belirli bir doğru parçası oluşturmaya eşdeğerdir . Orijinal geometrik problem böylece tamamen cebirsel bir probleme indirgenir. ${\ displaystyle \ çünkü (3 \ alfa)}$${\ displaystyle \ cos (\ alpha)}$

Kübik denklem kolayca edilebilir çıkarılmış De Moivre formül için karmaşık üstel fonksiyon . Euler formülüne göre aşağıdakiler geçerlidir:

${\ displaystyle e ^ {i \ alpha} = \ cos (\ alpha) + i \ sin (\ alpha)}$

ve her iki tarafı da 3'ün kuvvetine yükselterek, ve reel kısımları karşılaştırılarak denklem okunabilir. O gösterir hayali birimini karmaşık sayılar. ${\ görüntü stili (e ^ {i \ alpha}) ^ {3} = e ^ {3i \ alpha}}$${\ görüntü stili ben}$

Ayrıntılı olarak, cebirden aşağıdaki fikirler kullanılarak üç açıya bölünmenin imkansızlığının kanıtı gerçekleştirilebilir. En az 0 ve 1 ve isteğe bağlı bir nokta içeren bir dizi nokta ( karmaşık sayılar ) olsun . Bu düşünceler için, karmaşık sayıların bir düzlem olarak anlaşılabilmesi önemlidir - bunun aksine, gerçek sayılar sadece düz bir çizgi olarak anlaşılır. O zaman, noktanın , ancak ve ancak vücuttan bir karekökün eki ile oluşturulan bir cisim ( karmaşık sayıların gövdesi) içinde bulunuyorsa, bir pusula ve cetvelle noktalardan oluşturulabileceğini uygular.${\ görüntü stili M}$${\ görüntü stili z}$${\ görüntü stili z}$ ${\ görüntü stili M}$ ${\ displaystyle E \ altküme \ matbb {C}}$${\ displaystyle \ matematik {C}}$

${\ displaystyle K: = \ mathbb {Q} (M \ cup {\ overline {M}}) \ subset \ mathbb {C}}$

ortaya çıkar. Kabaca söylemek gerekirse, rasyonel sayılardan tüm toplamlar, farklar, ürünler ve bölümler oluşturularak oluşturulan miktardır . İşte tüm elemanlarının karmaşık eşleniği kümesi ve sembolü iki kümenin birleşimini temsil ediyor . Bir karekökün eklenmesi, öyle bir olması gerektiği anlamına gelir . Örneğin , rasyonel sayıların karekökünün eklenmesi, bunun rasyonel bir sayı olduğunu gösterir - buna karşılık, rasyonel sayıların tüm toplamları, farkları, ürünleri ve bölümlerinin sayısıdır . Ne zaman bir sözde vardır alan uzantısı . Açıları bir çift pergel ve cetvelle üçe bölme sorunu, bu nedenle, sayının , kareköklerin art arda eklenmesiyle elde edilebilen kısmi alanında olup olmadığı sorusuna indirgenebilir . Ancak, bu araçlar o genleşme derecesi arasında gelen 2'nin kuvvetlerine olmalıdır. Ama genel olarak öyle ${\ displaystyle \ mathbb {Q} (M \ cup {\ overline {M}})}$${\ displaystyle M \ cup {\ overline {M}}}$${\ displaystyle {\ overline {M}} = \ {{\ overline {m}} \ mid m \ in M ​​\}}$${\ görüntü stili M}$${\ displaystyle \ kupa}$${\ displaystyle w ^ {2} \ in K}$${\ görüntü stili E = K (w)}$${\ displaystyle \ mathbb {Q} ({\ sqrt {2}})}$${\ görüntü stili ({\ sqrt {2}}) ^ {2} = 2}$${\ displaystyle \ mathbb {Q} ({\ sqrt {2}})}$${\ görüntü stili {\ sqrt {2}}}$${\ displaystyle E \ orta K}$${\ displaystyle \ cos (\ alpha)}$${\ displaystyle \ matematik {C}}$${\ displaystyle \ mathbb {Q} (\ cos (3 \ alpha))}$${\ görüntü stili E}$${\ displaystyle \ matematik {Q}}$

${\ displaystyle [\ mathbb {Q} (\ cos (\ alpha), \ cos (3 \ alpha)): \ matbb {Q} (\ cos (3 \ alpha))] = 3 \ değil = 2 ^ {n } \ qquad {\ metin {herkes için}} \, n \ in \ mathbb {N},}$

bu da açıyı pergel ve cetvelle üçe bölmeyi imkansız kılıyor. Alan uzantısı Yani genel olarak sınıf 3, bu olarak görülebilir izler: polinom Eğer için indirgenebilir rasyonel sayılar üzerinde, bir rasyonel kök olurdu. nedeniyle eşdeğer olarak incelenebilir. Rasyonel kök teoreminden sonra sadece , , ve değerleri bu denklemin rasyonel sıfırları olarak bulunur. Bu değerlerin tümü, sıfır olarak değiştirilerek hariç tutulabilir. Bu nedenle üzerinde olmalıdır indirgenemez ve minimal polinom over 3 derece sahiptir. ${\ displaystyle \ mathbb {Q} (\ cos (\ alpha), \ cos (3 \ alpha)) \ mid \ mathbb {Q} (\ cos (3 \ alpha))}$${\ displaystyle p (x) = 4x ^ {3} -3x- \ cos (3 \ alpha)}$${\ displaystyle 3 \ alpha = {\ tfrac {\ pi} {3}}}$ ${\ displaystyle \ cos ({\ tfrac {\ pi} {3}}) = {\ tfrac {1} {2}}}$${\ displaystyle 8x ^ {3} -6x-1 = 0}$${\ görüntü stili \ pm 1}$${\ displaystyle \ pm {\ tfrac {1} {2}}}$${\ displaystyle \ pm {\ tfrac {1} {4}}}$${\ displaystyle \ pm {\ tfrac {1} {8}}}$${\ görüntü stili p (x)}$${\ displaystyle \ mathbb {Q} (\ cos ({\ tfrac {\ pi} {3}})) = \ mathbb {Q} ({\ tfrac {1} {2}}) = \ mathbb {Q}}$${\ displaystyle \ cos ({\ tfrac {\ pi} {9}})}$${\ displaystyle \ matematik {Q}}$

Açı olduğu gösterilebilir ise bir pergel ve cetvelle üçe ayrılır edilemez bir üstün numarası .${\ görüntü stili \ vartheta}$${\ displaystyle e ^ {i \ vartheta}}$

genelleme

Sorunun genelleştirilmesi, hangi açıların oluşturulabileceğini ve hangilerinin yapılamayacağını tam olarak karakterize etmektir. Eşdeğer sorunlar oldukları doğal sayılar a devre olarak cetvel ve pusula ya da bu normal çokgenler vasıtasıyla eşit büyüklükte parçalar ayrılabilir inşa edilebilir bulunmaktadır. İnşa edilebilir köşenin tam karakterizasyonu 1837'de Pierre Wantzel tarafından elde edildi ( Carl Friedrich Gauß ve Évariste Galois tarafından yapılan önemli hazırlık çalışmalarından sonra ) ve bu durumun ancak ve ancak iki ve çift olarak farklı Fermat'ın asal kuvvetinin bir ürünü olması durumunda geçerli olduğunu belirtir. sayılardır . Bir açı , ancak ve ancak iki ve çift olarak farklı Fermatyalı asal sayıların bir kuvvetinin çarpımı bölünmeyen ise eşit açılara bölünebilir. Özellikle, 3'ün bir Fermat asal sayısı olması nedeniyle, ancak ve ancak 3'e bölünemezse klasik olarak üçe bölünebilir. Örneğin, açı (yani ) üçe bölünebilir, çünkü and 3, 8'i bölmez. Öte yandan açı (yani ) durumunda ise 15 sayısı 3'e tam bölünebildiği için pergel ve cetvelle üçe bölünemez. ${\ görüntü stili n}$${\ görüntü stili n}$${\ görüntü stili n}$${\ görüntü stili n}$${\ görüntü stili {\ tfrac {2 \ pi} {N}}}$${\ görüntü stili n}$${\ görüntü stili n}$${\ görüntü stili N}$${\ görüntü stili {\ tfrac {2 \ pi} {N}}}$${\ görüntü stili N}$${\ görüntü stili {\ tfrac {\ pi} {4}}}$${\ displaystyle 45 ^ {\ circ}}$${\ displaystyle {\ tfrac {\ pi} {4}} = {\ tfrac {2 \ pi} {8}}}$${\ görüntü stili N = 15}$${\ görüntü stili {\ tfrac {2 \ pi} {15}}}$${\ displaystyle 24 ^ {\ circ}}$

Antik çağın matematiğinin ötesindeki ilk belirleyici adım, genç Gauss'un düzenli on yedi kenarlı yapının inşa edilebileceğini keşfetmesi sayesinde oldu .

Bilinen tek Fermat asal sayıları 3, 5, 17, 257 ve 65537'dir. Genel olarak, Fermat sayıları , kendileri ikinin kuvveti olan sayılardır . Tüm Fermat sayılarının bileşik sayılar olduğuna inanılmaktadır . ${\ displaystyle 2 ^ {m} +1}$${\ görüntü stili m = 2 ^ {q}}$${\ görüntü stili q> 4}$

Gauss ve Galois'in ileri teorilerine, açıların üç boyutlu bölünmesi problemi için ihtiyaç yoktur. Burada, üçüncü dereceden indirgenemez bir denklemi sağlayan bir yol uzunluğunun inşa edilemeyeceğini kabul etmek yeterlidir; çünkü her inşa edilebilir çizgi uzunluğu , ikinci dereceden denklemlerin birbiri ardına çözülmesiyle cebirsel olarak elde edilebilir, bu nedenle cebirsel olarak ikinin kuvvetidir.

amatörler tarafından çözüm girişimleri

Dolayısıyla açıyı pergel ve cetvelle üçe bölmenin imkansızlığı eskiden beri bilinmesine rağmen amatörler matematik dergilerini ve fakülteleri ispatlama çabalarıyla doldurmuşlardır. Bu fenomeni analiz eden Underwood Dudley , tipik trisektörü, sorunu gençliğinde duymuş (muhtemelen meslekten olmayanlar için üç klasik problemden en erişilebilir olanıdır) ve emekliliğinde onunla kurcalayan yaşlı bir adam olarak tanımlar. Yüzlerce kanıt denemesini toplayan Dudley, üç köşeli bölücüler arasında sadece iki kadın buldu .

Dudley, bir başka özelliğin de, sıradan insanların matematikte “imkansız”ın anlamını anlamaması ve bunun yerine onu bir meydan okuma olarak görmeleri olduğunu söyledi. Tipik olarak, matematik hakkında çok az bilgiye sahiptirler, ancak bu, tasarımlarındaki hataları bulmanın kolay olduğu anlamına gelmez. Karakteristik olarak, diyagramları çok karmaşıktır, ancak çoğu zaman geometrik bilgi ile büyük ölçüde basitleştirilebilir. Ayrıca, birçok patent ve gizlilik sorunu için önemsiz olmayan teknik uygulamalar için çözümlerinin önemine ikna olmuşlardır.

İnatçı açılı üçlü kişilerle başa çıkmak için pek çok yöntem denedikten sonra, Dudley, sorunun daha iyi anlaşılmasına bir katkı olarak (ya sadeliği ya da zarafeti için) onların çalışmalarını övmeyi önerdi. Ek olarak, onlara farklı açılar için deneyin hatasını gösteren bir bilgisayar çıktısının yanı sıra diğer açı üç bölenlerinin “yaklaşık çözümlerinin” örneklerini göndermelisiniz.

Klasik olmayan prosedürler

Kendinizi pergel ve cetveller için klasik yapı kurallarıyla sınırlamaz, aynı zamanda diğer yapım araçlarının ve matematiksel yardımcı nesnelerin kullanımına da izin verirseniz veya yaklaşık çözümlerden memnunsanız, herhangi bir açıyı bölmek için çok sayıda olası yöntem vardır. üç. Bunlardan bazıları aşağıdaki bölümlerde örnek olarak sunulmuştur.

Arşimet yöntemi

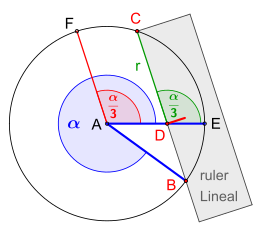
Arşimet bir pragmatistti, Liber Assumptorum'unda bir çözüm sundu . Bitişik çizimde gösterildiği gibi üçe bölünecek açı olsun . Ardından aşağıdaki gibi ilerleyin: ${\ görüntü stili \ alfa}$

1. Herhangi bir yarıçapa sahip bir yarım daire sarın .${\ görüntü stili A}$${\ görüntü stili r}$
2. Cetvel üzerinde belli bir mesafede iki işaret yapın .${\ görüntü stili r}$
3. Cetveli , iki işaretten biri noktadaki düz çizgide , diğeri noktadaki dairesel çizgide olacak şekilde yerleştirin ve çizgiyi çizin .${\ görüntü stili B}$${\ görüntü stili AD}$${\ görüntü stili D}$${\ görüntü stili C}$${\ displaystyle {\ üst çizgi {BD}}}$
4. Açı , aradığınız üçüncü açıdır .${\ görüntü stili \ beta}$${\ görüntü stili D}$

Gerekçesi olarak, not, çünkü cetvelin özel konumlandırma, hattın uzunluğu olduğu arasındaki mesafeye eşit işaretler, yani aynı zamanda şu şekilde bulunabilir dairenin yarıçapına eşit ve . Özellikle üçgen ikizkenardır, bu nedenle açı da oluşur. Üçgenin açısını en bir yandan, aynı olduğunu , diğer taraftan (üçgen açı toplamı) ikincil açısı böyledir, . Üçgen de ikizkenar olduğundan, açı da görünür ve bu üçgenin açısı eşittir . Şimdi dikkate alırsak, bu açıya endişeleri de ekleyelim . ${\ displaystyle {\ üst çizgi {CD}}}$${\ görüntü stili r}$${\ görüntü stili {\ üst çizgi {AC}}}$${\ görüntü stili {\ üst çizgi {AB}}}$${\ görüntü stili ACD}$${\ görüntü stili \ beta}$${\ görüntü stili A}$${\ görüntü stili ACD}$${\ görüntü stili C}$${\ displaystyle 180 ^ {\ circ} -2 \ beta}$${\ görüntü stili \ gama}$${\ görüntü stili \ gama = 2 \ beta}$${\ görüntü stili ABC}$${\ görüntü stili \ gama}$${\ görüntü stili B}$${\ görüntü stili A}$${\ displaystyle 180 ^ {\ circ} -2 \ gama}$${\ görüntü stili A}$${\ displaystyle 180 ^ {\ circ}}$${\ displaystyle \ alpha = 180 ^ {\ circ} - (180 ^ {\ circ} -2 \ gama) - \ beta = 2 \ gamma - \ beta = 4 \ beta - \ beta = 3 \ beta}$

Bu yöntemle her açının üç parçaya bölünebilmesi, kanıtlandığı gibi, klasik sorunun çözülemezliği ile çelişmemektedir, çünkü yukarıdaki yapı klasik olarak istenen kurallara göre yapılmamıştır. Cetvel üzerindeki bir işaret ve cetvelin akıllıca uygulanması klasik yapım yöntemlerine uymuyor. Farklı bir alet seti kullanılmış ve olası yapılar alet setine bağlıdır.

Pappos yöntemi

Arasında Neusis yapı Pappos üçe bölünmesi için dar açıların, aşağıda tarif edilen, söz konusu geç gelen antik .

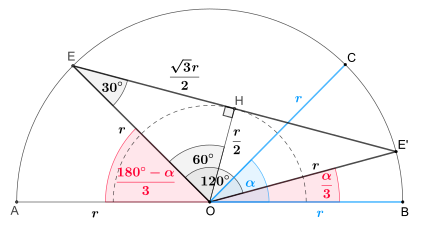
Açı bölünecek , sağdaki resme bakın: ${\ görüntü stili \ açı {KÖTÜ} = 3 \ alfa}$

İki açılı bacak çizildikten sonra ve herhangi bir uzunluk bacak üzerinde çizgi olarak belirlenebilir . Bir paralel ab hem de dikey ab temel nokta ile ilgili takip. Şimdi, uzunluğu eşit olduğu cetvel, seçilmektedir, tepe kadar hareket paralel olarak olup, uzunluğu parça olarak apeksinden kesintileri ve cetvelin böylece kenar uzanır. Bu şekilde bulunan açı aradığınız açıdır.${\ görüntü stili {\ üst çizgi {AB}}}$${\ displaystyle {\ üst çizgi {AD}}}$${\ görüntü stili a}$${\ görüntü stili {\ üst çizgi {AC}}}$${\ displaystyle {\ üst çizgi {AD}}}$${\ görüntü stili {\ üst çizgi {AB}}}$${\ görüntü stili C}$${\ görüntü stili C}$${\ görüntü stili E}$${\ görüntü stili {\ üst çizgi {AB}}}$${\ görüntü stili 2a}$${\ görüntü stili G}$${\ görüntü stili {\ üst çizgi {AB}}}$${\ görüntü stili 2a}$${\ displaystyle {\ üst çizgi {CE}}}$${\ görüntü stili F}$${\ görüntü stili A}$${\ displaystyle \ açı {ÇANTA}}$${\ görüntü stili \ alfa.}$

Bu açı , kirişin çevre açısına eşit alternatif açılar olduğundan ve daire açısı ayarlandıktan sonra ilişkili merkez açıya eşit olduğundan, üçgen ikizkenar olduğundan, bu açı da geçerlidir, ancak farka eşittir ve bu nedenle doğrudur.${\ displaystyle \ açı ÇANTA =: \ beta}$${\ görüntü stili \ açı AGC = \ açı FGC,}$${\ displaystyle {\ overline {CF}},}$ ${\ görüntü stili \ açı FMC}$${\ görüntü stili 2 \ beta.}$${\ displaystyle \ üçgen AMC}$${\ görüntü stili \ açı FAC = 2 \ beta.}$${\ Displaystyle \ Açı KÖTÜ- \ BAG açısı = 3 \ alpha - \ beta,}$${\ displaystyle 2 \ beta = 3 \ alfa - \ beta}$${\ görüntü stili \ beta = \ alfa.}$

Kesik çizgiler ve merkez nokta inşaat için gerekli değildir, sadece kanıt içindir. ${\ görüntü stili M}$

Tomahawk ile bölün

Tomahawk bakış matematiksel açıdan, iki dik çizgi ve düz çizgiler birine bitişik bir yarım daire oluşur, bir rakamdır; arka uç yarım dairenin yarıçapı kadardır (çizime bakın). Tomahawk adı, figürün belli belirsiz bir tomahawk'a (bir Hint savaş baltası) benzediği gerçeğinden gelir . Bir açıyı tomahawk yardımıyla üç parçaya bölmek için, onu "gövdesi" (tomahawk'ın sapı) apeksten geçecek ve yarım daire (tomahawk'ın bıçağı) olacak şekilde konumlandırmanız gerekir (bkz. ) ve "kanca" ( tomahawk'ın arka ucu) açının bacaklarına dokunur. Bu pozisyonda tutamak, bacaklardan biri ile başlangıç ​​açısının tam olarak üçte biri olan bir açı oluşturur. Yarım dairenin merkezinin açı ucu ile bağlantısı, başlangıç ​​açısının ikinci ve üçüncü üçte birini böler. Tomahawk, yaratılması gereken bir figür olduğundan, bu yöntem klasik yapım kurallarına (cetvel ve pusula) uymamaktadır.

Bir açıyı karakalem kullanarak doğrudan üçe bölmek mümkün değilse (bkz. Şekil 3) verilen açı çok küçük olduğundan küçük açının üçe bölünmesi yapılabilir. ilişkili büyük ikincil açının üç parçalı bölümünden . Eğer bir açı düşünün yarıçapında bir yarım daire üzerinde ikincil açı ile elde edersiniz açının büyüklüğüne bağlı değildir sabit açı (çizim). Bu açı, yüksekliği olan bir ikizkenar üçgenin parçasıdır . Bu daha sonra bir sonraki paragrafta açıklanan yapı ile sonuçlanır. ${\ görüntü stili \ alfa}$${\ görüntü stili r}$${\ displaystyle {\ tfrac {2} {3}} (180 ^ {\ circ} - \ alpha) + {\ tfrac {2} {3}} \ alpha = 120 ^ {\ circ}}$${\ görüntü stili \ alfa}$${\ displaystyle 120 ^ {\ circ}}$${\ görüntü stili {\ tfrac {r} {2}}}$

• 

  Şekil 1
  Bir tomahawk ile bir açının üçe kesiti. Aynı boyuttaki üçgenler kırmızı / sarı / yeşil renkle vurgulanır.

• 

  Şekil 2
  90 ° (kırmızı) ile 180 ° (mavi) arasındaki açıların üç yönlü bölünmesi için şablon (şematik gösterim)

• 

  Şekil 3 Yüksekliği olan
  ikizkenar üçgen${\ displaystyle \ üçgen EOE ^ {\ asal}}$${\ görüntü stili | OH | = {\ tfrac {r} {2}}}$

• 

  Şekil 4
  Küçük açılar için tomahawk'ın konumu (açık mavi)

Çapı çizerek , ikiye bölerek ve üzerine yarım daire çizerek başlar (bkz. Şekil 4) . Bunu iki açılı ayağı ile verilen açıya girmek takip eder . Aşağıdaki gibi Şimdi, Tomahawk konumlandırılmış "kanca" yolda bulunan yarım daire üst açılı bacak dokunur ve "sap" merkezinden geçen iki yolun çizilmesi ile , ve üç ilâ elde ek açısının bölünmesi . Açının üç yönlü bir bölümünü elde etmek için nokta şimdi dairesel yay üzerine yansıtılır . Bu amaç için, yarıçapı içinde yarım ve bir yarı-daire çevresinde gelen kesişim noktası çizilen bu sonuçlar . Son olarak, bir yarım daire lüzum bir yarıçap ile , kesişim noktasından ve düz hat boyunca yaya . Bu şekilde oluşturulan kesişme noktası , noktanın sanal rota üzerindeki yansımasıdır . Böylece oluşturulan açı, verilen açının tam olarak üçte biri kadardır . ${\ görüntü stili {\ üst çizgi {AB}}}$${\ görüntü stili O}$${\ görüntü stili {\ üst çizgi {AB}}}$${\ görüntü stili \ açı BOC}$${\ displaystyle {\ üst çizgi {AO}},}$${\ görüntü stili O.}$${\ displaystyle {\ üst üste {DO}}}$${\ displaystyle {\ üst çizgi {EO}}}$${\ görüntü stili \ açı {COA}}$${\ görüntü stili \ açı BOC}$${\ görüntü stili E}$${\ görüntü stili OBC}$ ${\ displaystyle {\ üst çizgi {AO}}}$${\ görüntü stili F}$${\ görüntü stili O}$${\ görüntü stili F}$${\ görüntü stili G}$${\ görüntü stili G}$${\ displaystyle {\ overline {GO}}}$${\ görüntü stili H}$${\ görüntü stili E}$${\ görüntü stili H}$${\ görüntü stili OBC}$${\ görüntü stili E '}$${\ görüntü stili E}$${\ displaystyle {\ üst çizgi {HO}}}$${\ displaystyle \ açı {BOE '}}$${\ görüntü stili \ açı {BOC}}$

Dik açılı üçgen cetvelle bölme

1932'de Ludwig Bieberbach , kübik yapıların öğretimi üzerine çalışmasını yayınladı . İçinde şöyle açıklıyor:

Açı üçe bölünmelidir. eğer ayarlarsan ${\ görüntü stili \ delta}$

${\ displaystyle \ alpha = \ cos (\ delta)}$  ve  ${\ displaystyle z = \ cos \ sol ({\ frac {\ delta} {3}} \ sağ),}$

bu denkleme yol açar

${\ displaystyle z ^ {3} - {\ frac {3} {4}} z - {\ frac {\ alpha} {4}} = 0.}$

Soldaki animasyonlu yapının aşağıdaki açıklaması - von Bieberbach'ınkine dayalıdır - açının tam üç katına kadar devamını içerir.

Merkez noktasının etrafındaki ilk birim daire (Bieberbach'ın argümantasyonunun temeli, prensipte herhangi bir yarıçapa sahip bir daire de uygundur) , birinci açı ayağı ve ardından ikinci birim daire ile başlar . Şimdi çapı genişletilmiş gelen kesişme noktasında sonuçlanan ikinci birim çember, dairesel hattına . Bunu yarıçapla birlikte çevredeki yay ve üçüncü açının ikinci açı ayağının içeri çekilmesi takip eder , bu da nokta ile sonuçlanır . ${\ görüntü stili A}$${\ displaystyle {\ overline {BP}}}$${\ görüntü stili P}$${\ displaystyle {\ overline {BP}}}$${\ görüntü stili P}$${\ görüntü stili O}$${\ görüntü stili P}$${\ displaystyle {\ üst üste {PB}}}$${\ görüntü stili \ delta}$${\ görüntü stili C}$

Şimdi, sözde ek inşaat araçları kullanılmaktadır, gösterilen örnekte bu, set karedir . Bu şimdi çizime şu şekilde yerleştirilir: Açının tepe noktası açı ayağındaki noktayı belirler , üçgenin bir ayağı noktadan geçer ve diğeri birim çembere teğet olur . Bu bağlantı noktasından sonra ile ve çekme teğet gelen yaklaşık birim çembere , yukarıda bahsedilen sağ - açılı kanca görüntülenir . Çizgilerin içerdiği açı ve bu nedenle kesindir . Bu paralellik devam itibaren yanında sonuçlanan değişim açısı veya Z-açı ve nokta yay üzerinde etrafında . Başka bir paralel ab arasındaki temas noktası yeniden tanımlar teğet ve birim çember . Son olarak, çizmek düz bir çizgi boyunca o kadar keser dairenin yayı içinde . ${\ displaystyle 90 ^ {\ circ}}$${\ displaystyle {\ overline {PC}}}$${\ görüntü stili S}$${\ görüntü stili O}$${\ görüntü stili A}$${\ görüntü stili O}$${\ görüntü stili S}$${\ görüntü stili S}$${\ görüntü stili A}$${\ displaystyle {\ overline {OS}}}$${\ displaystyle {\ üst çizgi {PS}}}$${\ görüntü stili {\ tfrac {\ delta} {3}}}$${\ displaystyle {\ overline {OS}}}$${\ görüntü stili P}$ ${\ görüntü stili {\ tfrac {\ delta} {3}}}$${\ görüntü stili D}$${\ görüntü stili P}$${\ displaystyle {\ overline {OS}}}$${\ görüntü stili A}$${\ görüntü stili E}$${\ görüntü stili A}$${\ görüntü stili P}$${\ görüntü stili E}$${\ görüntü stili P}$${\ görüntü stili F}$

Yani açı nedeniyle ${\ görüntü stili \ delta}$

${\ displaystyle {\ overline {PS}} = 2 \ cdot \ cos \ sol ({\ frac {\ delta} {3}} \ sağ)}$

tam olarak üçe bölünmüştür.

eğriler

Bir trisectrix, bir pusula ve cetvel ile bir açının tam üçte birini sağlayan bir eğridir . Eğrinin pergel ve cetvel dışındaki araçlarla varlığı veya oluşturulabilirliği burada verilmiştir ve bu eğrinin tek ek yardım olarak yardımıyla bir açıyı üçe bölmek mümkündür. Pergeller ve cetvellerle yapılan saf yapının aksine, noktalar yalnızca düz çizgiler ve dairelerle kesişerek değil, aynı zamanda verilen eğri ile düz çizgiler ve dairelerle kesişerek de oluşturulabilir. Eğri noktalarının tamamı pergel ve cetvellerle oluşturulamaz, bu nedenle böyle bir eğrinin kullanılması, açı üçe bölme için klasik kuralların ihlalidir.

Tek bir hiperbol yardımıyla üç parçalı farklı açılar

→ Ana madde: Hiperbol, Hiperbol Trisektrix olarak

1902'de K. Matter açının üçe bölünmesi üzerine bir makale yayınladı . İçinde sadece bir hiperbol ile farklı açıları üçe bölmeyi mümkün kılan bir yöntem gösteriyor.

En ünlü trisektrisin seçimi

• Hippias'ın Trisffektix'i (MÖ 5. yy) ve
• Arşimet spiralleri (MÖ 3. yüzyıl) bu tür eğrilerin en eski örnekleri arasındadır.
• Hiperbol Trisektrix olarak , bu eğri Pappos tarafından MS 4. yüzyılda bu sorunu çözmek için kullanılmıştır.
• Parabol , René Descartes tarafından 1637'den La Geometria adlı eserinde tanımlanan Trisektrix olarak .
• Fransız avukat Étienne Pascal tarafından 1637 civarında bulunan Trisektrix olarak Pascal salyangozu .
• İtalyan Cizvit Tommaso Ceva (1648-1736) tarafından keşfedilen Ceva Cycloid , aynı zamanda herhangi bir açının üçe bölünmesini sağlar.
• Maclaurin-Trisektrix , 1742'de Colin Maclaurin tarafından incelenmiştir .
• Trisektrix von Longchamps , Fransız matematikçi Gohierre de Longchamps'tan (1842–1906) geliyor.

Origami ile açıyı üçe bölmek

Açının üç boyutlu bölünmesi klasik geometri aletleri ile mümkün olmasa da origami kağıt katlama tekniği ile iş çözülebilir. Bunun için dikdörtgen veya kare bir kağıt yaprağı kullanılır. Bir açıyı üçe bölmek için yaprağın altı katı gerekir. ${\ displaystyle 0 ^ {\ circ} <3 \ alpha <90 ^ {\ circ}}$

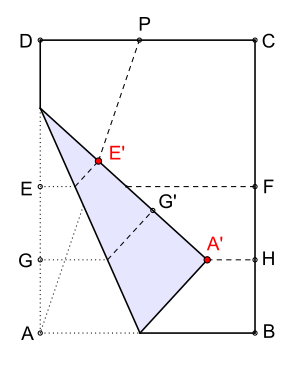
İlk olarak levha ortadan katlanır (bkz. resim 1), iki levhanın kenarında noktalar vardır ve alternatif olarak çizginin uzunluğu serbestçe seçilebilir . Katlama takip eder, yarıya indirir, çizgi noktası şimdi çizgi üzerinde istendiği gibi belirlenir (bkz. Resim 2) ve ardından tabaka 'den ' ye katlanır. Bu açıyı verir tepe noktasında${\ görüntü stili E}$${\ görüntü stili F.}$${\ displaystyle {\ üst çizgi {EF}}}$${\ displaystyle {\ overline {AE}}}$${\ displaystyle {\ üst çizgi {GH}},}$${\ displaystyle {\ overline {AE}}.}$${\ görüntü stili P}$${\ displaystyle {\ üst çizgi {CD}}}$${\ görüntü stili A}$${\ görüntü stili P}$${\ görüntü stili 3 \ alfa}$${\ görüntü stili A.}$

Şimdi belirleyici dördüncü kat, (resim 3) aşağıdaki bölmek üçe açı ilk köşe yerleştirerek, kat üzerinde ve nokta kat üzerinde . Sayfa üzerinde nokta işaretlendikten sonra köşe geriye doğru bükülür ve kesişme noktası işaretlenir - dördüncü katlama ile oluşturulur - levha tekrar dikdörtgen şeklini alır. ${\ görüntü stili 3 \ alfa}$${\ görüntü stili A}$${\ displaystyle {\ üst çizgi {GH}}}$${\ görüntü stili E}$${\ displaystyle {\ overline {AP}}}$${\ görüntü stili A '}$${\ görüntü stili A}$${\ görüntü stili I}$${\ displaystyle {\ üst çizgi {GH}}}$

Son olarak kapağı, (resim 4) üzerinden ve bir tane ile . Çizgileri katlayın ve açıyı üç (tam olarak) eşit parçaya bölün . ${\ görüntü stili A}$${\ görüntü stili I}$${\ görüntü stili A}$${\ görüntü stili A '}$${\ displaystyle {\ overline {AG '}}}$${\ displaystyle {\ üst çizgi {AA '}}}$${\ görüntü stili 3 \ alfa}$

• 

  Resim 1
  İlk iki kat çizgisini katlayın , sayfanın ortasında olması gerekmez ${\ displaystyle {\ üst çizgi {EF}}}$

• 

  Resim 2
  Üçüncü kat, açıyı sağlar${\ görüntü stili 3 \ alfa}$

• 

  Resim 3
  Önemli dördüncü kat, yukarı ve aşağı köşe${\ görüntü stili A}$${\ displaystyle {\ üst çizgi {GH}}}$${\ görüntü stili E}$${\ displaystyle {\ overline {AP}}}$

• 

  Fotoğraf 4
  Katlama çizgileri ve açıyı üç eşit parçaya bölün${\ displaystyle {\ overline {AG '}}}$${\ displaystyle {\ üst çizgi {AA '}}}$${\ görüntü stili 3 \ alfa}$

Açıyı üç parçaya bölmek için esnek bir cetvel kullanın

Bu yöntemde, üç boyutlu bir çizgi ile dört noktada kesişen silindirik bir yüzeye bir sarmal uygulanır. İki iç kesişme noktası, iki dış olanın verdiği açıyı böler. Daha yakından incelendiğinde , Hippias'ın Quadratrix yöntemiyle yapının benzerliği görülür . Öklid araçları - pergeller ve cetveller - yerine, silindirin belirli bir daire merkezine sahip silindirik bir gövde , esnek bir cetvel (örneğin şerit metre ) ve alternatif olarak ör. B. bir durdurma braketi kullandı. ${\ görüntü stili M}$

yöntem

Öncelikle her açı ayağı çizilir merkezinden daire (Şekil 1 e bakınız) ve açı üçüncü bir olan belirlenmiş açı ile bacak . İki (kırmızı) çizgileri daha sonra çekilir ve örneğin, alternatif olarak, esnek cetvel kullanarak ya da dış yüzeyinde B. (dik açılı) bir durdurma braketi kullanarak. ${\ görüntü stili M}$${\ displaystyle {\ üst çizgi {MA}}}$${\ görüntü stili 3 \ alfa}$${\ displaystyle {\ üst çizgi {MB}}}$${\ görüntü stili {\ üst çizgi {AC}}}$${\ displaystyle {\ üst çizgi {BD}}}$

Bir sonraki adım, sarmal çizgiyi (yeşil) silindirik yüzeye uygulamaktır (bkz. Şekil 2). Esnek cetvel silindirin kenarına yerleştirilir ve sabitlenir. Bunu, cetvelin genişliğine karşılık gelen aynı aralıkta beş sargı takip eder. Sarmal, cetvelin serbest kenarında adım adım çizilir. Şimdi sarmalın ilk sargısı ve dördüncü sargı ile kesişme noktaları işaretlenmiştir. ${\ görüntü stili h,}$${\ görüntü stili E}$${\ görüntü stili F}$

Esnek cetvel şimdi silindirik yüzeye yerleştirilir (bkz. Şekil 3), böylece cetvelin kenarı (açık mavi) noktalardan geçer ve kesişme noktaları ve helisel çizgi üzerinde işaretlenir . Bu durumda, bu çizgi - aynı zamanda çok geniş aralıklı bir sarmal - iki noktanın en kısa mesafesi ve sonuç esnek cetveli veya alternatif olarak z'yi kullanır. B., yolları bir durdurma desteği kullanılarak ve yanı sıra ve girdi. ${\ görüntü stili E}$${\ görüntü stili F}$${\ görüntü stili G}$${\ görüntü stili I}$${\ görüntü stili E}$${\ görüntü stili F.}$${\ displaystyle {\ üst çizgi {IJ}}}$${\ displaystyle {\ üst çizgi {JM}}}$${\ displaystyle {\ üst çizgi {GH}}}$${\ displaystyle {\ üst çizgi {HM}}}$

Bu nedenle açı tam olarak üç parçaya bölünmüştür. ${\ görüntü stili | AJ | = | JH | = | HB |}$${\ görüntü stili 3 \ alfa}$

• 

  Şekil 1,
  bir açı çizimi ve iki (kırmızı) yollarının ve esnek cetvel veya alternatif olarak bir (dikdörtgen) durdurma dirseği kullanılarak ${\ görüntü stili 3 \ alfa}$${\ görüntü stili {\ üst çizgi {AC}}}$${\ displaystyle {\ üst çizgi {BD}}}$

• 

  Şekil 2
  Vida çizgisini (yeşil) esnek cetvel yardımıyla dış yüzeye çizin .

• 

  Şekil 3
  Esnek cetvel yardımıyla üç boyutlu bir çizgi çizin, iç kesişim noktalarını sarmal çizgi ile dairesel alana yansıtın ${\ görüntü stili G}$${\ görüntü stili I}$

Yaklaşım yöntemi

Albrecht Dürer'in bölmeyi üçe yakınlaştırması

1906'da Karl Hunrath, Heidelberger Texte zur Mathematikgeschichte dergisinde Dürer'in 1525'ten itibaren üç boyutlu açıların bölünmesinin yaklaşık çözümünü içeren bir çalışma yayınladı .

İnşaat açıklaması

Belirli bir de bir daire sektörü bir merkez noktası olan bir orta nokta açısı daha büyük , kiriş ayrılmıştır içine ve üçte. Bunu, kesişme noktaları veya dairesel yay ile sonuçlanan ve içinde iki dikmenin kurulması takip eder . Şimdi yarıçaplı dairesel yay ab ve yarıçapı olan ikinci bir ab bunlar kadar çekilir kesim içine ya da içine kiriş . Yol üçte sonra noktasına yakın ve hat noktasına yakın , kesişme noktaları ve noktalarının çıkıntı ve noktası malzemeleri olan dairesel bir yay için ve bağlantı boruları (kırmızı) ile ve ve merkez açısı bölmek yaklaşık üç eşit parçaya bölünür. ${\ görüntü stili O}$ ${\ görüntü stili \ açı {AOB}}$${\ displaystyle 90 ^ {\ circ}}$${\ görüntü stili {\ üst çizgi {AB}}}$${\ görüntü stili C}$${\ görüntü stili D}$${\ görüntü stili {\ üst çizgi {AB}}}$${\ görüntü stili C}$${\ görüntü stili D}$${\ görüntü stili E}$${\ görüntü stili F}$${\ displaystyle {\ overline {AE}}}$${\ görüntü stili E}$${\ displaystyle {\ üst çizgi {BF}}}$${\ görüntü stili F}$${\ görüntü stili {\ üst çizgi {AB}}}$${\ görüntü stili E_ {1}}$${\ görüntü stili F_ {1}}$${\ displaystyle {\ üst çizgi {CE_ {1}}}}$${\ görüntü stili E_ {1}}$${\ displaystyle {\ üst çizgi {DF_ {1}}}}$${\ görüntü stili F_ {1}}$${\ görüntü stili G_ {1}}$${\ görüntü stili H_ {1}.}$${\ görüntü stili G_ {1}}$${\ görüntü stili H_ {1}}$${\ görüntü stili G}$${\ görüntü stili H.}$${\ görüntü stili G}$${\ görüntü stili O}$${\ görüntü stili H}$${\ görüntü stili O}$${\ görüntü stili \ açısı AOB}$

Bu sonuca iki yineleme adımı ile ulaşılır . İlk yinelemeden sonra açılar ve sonuç${\ görüntü stili \ açı {EOA},}$ ${\ displaystyle \ açı {FOE}}$${\ görüntü stili \ açı {BOF}.}$

Çizilen noktalar ve ortadaki çizgi inşaat için gerekli değildir, sadece Hunrath tarafından ayrıntılı olarak tartışılan ispata hizmet ederler.${\ görüntü stili K, L, M, N}$${\ görüntü stili Q}$${\ görüntü stili {\ üst çizgi {OI}}}$

Hata değerlendirmesi

Dürer'in yaklaşık çözümü, açılar için yalnızca çok küçük mutlak hatalar gösteriyor${\ displaystyle 0 ^ {\ circ} <2 \ alpha \ leq 180 ^ {\ circ}}$ ${\ görüntü stili F_ {a}.}$

Açının Üç Bölümlü Dürer'ın göre mutlak hata açısı${\ görüntü stili 2 \ alfa}$ ${\ görüntü stili F_ {a}}$${\ displaystyle \ beta = \ GOA açısı = \ BOH açısı,}$ ${\ displaystyle 1 '' = 0 {,} 0002 {\ üst çizgi {7}} \ matematik {^ {\ circ}}}$
açı ${\ görüntü stili 2 \ alfa}$	açı ${\ görüntü stili 2 \ alfa / 3}$	açı ${\ görüntü stili \ beta}$	${\ görüntü stili F_ {a}}$	${\ görüntü stili F_ {a}}$
0${\ displaystyle 30 ^ {\ circ}}$	${\ displaystyle 10 ^ {\ circ}}$	0${\ displaystyle 9 ^ {\ circ} \; 59 '\; 59 {,} 992' '}$	${\ displaystyle -0 {,} 007 ''}$	${\ displaystyle -0 {,} 0000019 {\ overline {4}} \ matrm {^ {\ circ}}}$
0${\ displaystyle 45 ^ {\ circ}}$	${\ displaystyle 15 ^ {\ circ}}$	${\ displaystyle 14 ^ {\ circ} \; 59 '\; 59 {,} 879' '}$	${\ displaystyle -0 {,} 12 ''}$	${\ displaystyle -0 {,} 0000 {\ overline {3}} \ matrm {^ {\ circ}}}$
0${\ displaystyle 60 ^ {\ circ}}$	${\ displaystyle 20 ^ {\ circ}}$	${\ displaystyle 19 ^ {\ circ} \; 59 '\; 59 {,} 093' '}$	${\ displaystyle -0 {,} 906 ''}$	${\ displaystyle -0 {,} 000251 {\ overline {6}} \ matematik {^ {\ circ}}}$
0${\ displaystyle 90 ^ {\ circ}}$	${\ displaystyle 30 ^ {\ circ}}$	${\ displaystyle 29 ^ {\ circ} \; 59 '\; 44 {,} 504' '}$	${\ displaystyle -15 {,} 495 ''}$	${\ displaystyle -0 {,} 0043041 {\ overline {6}} \ matematik {^ {\ circ}}}$
${\ displaystyle 120 ^ {\ circ}}$	${\ displaystyle 40 ^ {\ circ}}$	${\ displaystyle 39 ^ {\ circ} \; 58 '\; 4 {,} 427' '}$	${\ displaystyle -1 '\; 55 {,} 572' '}$	${\ displaystyle -0 {,} 03210 {\ overline {3}} \ matrm {^ {\ circ}}}$
${\ displaystyle 150 ^ {\ circ}}$	${\ displaystyle 50 ^ {\ circ}}$	${\ displaystyle 49 ^ {\ circ} \; 50 '\; 56 {,} 209' '}$	${\ displaystyle -9 '\; 3 {,} 79' '}$	${\ displaystyle -0 {,} 151052 {\ overline {7}} \ matrm {^ {\ circ}}}$
${\ displaystyle 180 ^ {\ circ}}$	${\ displaystyle 60 ^ {\ circ}}$	${\ displaystyle 59 ^ {\ circ} \; 28 '\; 22 {,} 498' '}$	${\ displaystyle -31 '\; 37 {,} 501' '}$	${\ displaystyle -0 {,} 5270836 {\ overline {1}} \ matrm {^ {\ circ}}}$

Açının yinelemeli ikiye bölünmesi yoluyla yaklaşıklık

Bu daha az verimli ama çok daha basit yöntem, geometrik seriyi kullanır.

${\ displaystyle {\ frac {\ alpha} {3}} = \ alpha \ cdot \ sol ({\ frac {1} {2}} - {\ frac {1} {4}} + {\ frac {1} {8}} - {\ frac {1} {16}} + {\ frac {1} {32}} - {\ frac {1} {64}} + \ nokta \ sağ)}$

Dokuz yinelemeden sonra örnek açı${\ displaystyle 60 ^ {\ circ}}$

${\ displaystyle 60 ^ {\ circ} \ cdot \ sol ({\ frac {1} {2}} - {\ frac {1} {4}} + {\ frac {1} {8}} - {\ frac {1} {16}} + {\ frac {1} {32}} - {\ frac {1} {64}} + {\ frac {1} {128}} - {\ frac {1} {256} } + {\ frac {1} {512}} \ sağ) = 60 ^ {\ circ} \ cdot {\ frac {171} {512}} = 20 {,} 0390625 ^ {\ circ}}$

Aşağıdaki formülün geçerli olduğuna dikkat edilmelidir:

${\ displaystyle \ toplam _ {k = 1} ^ {n} {\ frac {(-1) ^ {k-1}} {2 ^ {k}}} = {\ frac {1} {3}} - {\ frac {(-1) ^ {n}} {3 \ cdot 2 ^ {n}}}.}$

Gösterimi ile dolaylı bir bağlantı da vardır içinde ikili sistemde . ${\ displaystyle {\ frac {1} {3}} = [0 {,} 010101 \ nokta] _ {2} = [0 {,} {\ overline {01}}] _ {2}}$

0 ° ila 90 ° arasındaki açılar için yaklaşıklık

2011'de Chris Alberts, Rouben Rostamian'a ( Maryland Üniversitesi, Baltimore County ) üç köşeli bir açı için olağanüstü derecede iyi bir yaklaşım gönderdi .

Rostamian, Alberts'in yapısını yeniden formüle etti ve yeniden düzenledi, ancak orijinalinden farkların sadece kozmetik olduğunu söylüyor. Yapım açıklamasının başında, bu yapının hiçbir resminin neden görülmediğinin nedenlerini de gösterdiği bir açıklamaya ("buradaki açıklama") atıfta bulunur. Bununla birlikte, aşağıda gösterilen yapı, yalnızca Rostamian'ın açıklamasının yardımıyla mümkündür.

yapı

(Tercüme)

Yay bak çemberin üzerinde olan (resme bakın) merkezli. Açının ve dereceler arasında olduğunu varsayarak bölmek için aşağıdakileri yapın:${\ görüntü stili AB}$${\ görüntü stili C}$${\ görüntü stili O}$${\ görüntü stili \ açı {AOB}}$${\ görüntü stili 90}$${\ görüntü stili \ açı {AOB}}$

1. Bir daire çizin çevresinde bir yarı çapa sahip çizgilerle kesişim noktalarını veya vardır ya da${\ görüntü stili {C '}}$${\ görüntü stili O}$${\ displaystyle {\ tfrac {1} {3}} {\ overline {OA}};}$${\ displaystyle {\ overline {OA}}}$${\ displaystyle {\ overline {OB}}}$${\ görüntü stili {A '}}$${\ görüntü stili {B '}.}$
2. Bir daire çizin (yeşil renkte) noktası boyunca${\ görüntü stili {C ''}}$${\ görüntü stili {B '}}$${\ görüntü stili O.}$
3. Parçanın orta noktası olsun Kesişme noktalarının bulunduğu çembere paralelden dairesel doğruya doğru bir doğru çizin veya${\ görüntü stili E}$${\ displaystyle {\ overline {OB '}}.}$${\ görüntü stili E}$${\ displaystyle {\ overline {OA}}}$${\ görüntü stili {C ''}}$${\ görüntü stili {C '};}$${\ görüntü stili P}$${\ görüntü stili R.}$
4. Bu olsun hattının orta noktası. Bir çizgi çizin boyunca bu kadar kesişen daire içinde .${\ görüntü stili M}$${\ displaystyle {\ overline {PR}}.}$${\ görüntü stili {B '}}$${\ görüntü stili M,}$${\ görüntü stili {C '}}$${\ görüntü stili N}$
5. Buna paralel bir çizgi çizin ve üzerindeki noktayı seçin .${\ görüntü stili {B '}}$${\ displaystyle {\ overline {OA}}}$${\ görüntü stili F}$${\ displaystyle {\ overline {NB '}} = {\ overline {NF}}}$
6. Güzergahı uzat çemberin kadar içinde kesikler.${\ displaystyle {\ overline {NF}},}$${\ görüntü stili C}$${\ görüntü stili G}$
7. Çizgiyi çizin ve daire ile kesişene kadar uzatın .${\ displaystyle {\ overline {GO}}}$${\ görüntü stili {C '}}$${\ görüntü stili {H}}$

Not: Eğer çizim yakından bakarsanız, görebilirsiniz hatlar ve yapamaz örtüşme, yani H. doğrusal değildir .${\ displaystyle {\ overline {GO}}}$${\ displaystyle {\ üst çizgi {GN}}}$

8. Bu olsun çap noktasının karşısında . Daire içinde bir çizgi çizin paralel ve noktasını seçmek mesafe o kadar üzerinde olan.${\ görüntü stili D}$ ${\ görüntü stili {B '}}$${\ görüntü stili {C '}.}$${\ görüntü stili D}$${\ displaystyle {\ overline {OA}}}$${\ görüntü stili J}$${\ görüntü stili | HD | = {\ üst çizgi {HJ}}}$

Not: Rota , rotanın bir uzantısı değildir${\ displaystyle {\ üst çizgi {HJ}}}$${\ displaystyle {\ üst çizgi {GH}}.}$

9. Güzergahı uzat çemberin kadar içinde kesikler.${\ displaystyle {\ üst çizgi {HJ}},}$${\ görüntü stili C}$${\ görüntü stili K}$
10. Noktayı elde etmek için piste yansıtın .${\ görüntü stili K}$${\ displaystyle {\ overline {OA}},}$${\ görüntü stili T}$

Açı neredeyse açının üçte birine eşittir${\ görüntü stili \ açı {AOT}}$${\ görüntü stili \ açı {AOB}.}$

Başarısızlık analizi

Rostamian, diğer şeylerin yanı sıra aşağıdaki sonuçlara sahip bir hata analizi gerçekleştirdi: Yukarıdaki yapım adımları (1. – 10.) Üç yaklaşıklık seviyesi içerir, i. H. ve arasındaki aralıkta üç farklı hata boyutu : ${\ displaystyle 0 ^ {\ circ}}$${\ displaystyle 90 ^ {\ circ}}$

• Adım 1: 5. adımdan sonra, açı ile tam olarak üçte bir olan açı arasındaki fark max.${\ görüntü stili \ açı {F {B '} N}}$${\ displaystyle 0 {,} 7 ^ {\ circ}.}$
• Adım 2: 7. adımdan sonra, açı ile tam bölünmüş açı arasındaki fark sadece maks.${\ görüntü stili \ açı {{A '} OH}}$${\ displaystyle 0 {,} 00013791 ^ {\ circ}.}$
• Adım 3: 10. adımdan sonra açı, maks.${\ görüntü stili \ açı {AOT}}$${\ displaystyle \ sol (1 {,} 33 \ cdot 10 ^ {- 16} \ sağ) ^ {\ circ}.}$

Gösterilen yapı, dinamik geometri yazılımı (DGS) GeoGebra ile yapılmıştır ; Bu durumda, dereceler on üç ondalık basamakla gösterilir. Açıdaki çok küçük hatalar, diğer bir deyişle farklılıklar bu nedenle GeoGebra tarafından her zaman gösterilir. ${\ görüntü stili \ açı {AOT},}$${\ görüntü stili {\ tfrac {\ alpha} {3}} - \ beta,}$${\ displaystyle 0 ^ {\ circ}}$

Mutlak hatanın netleştirilmesi

Maks.'nin fark değeri , akorun - gösterilmeyen - mutlak bir hatasına karşılık gelir ve bu da aşağıdaki gibi sonuçlanır: ${\ displaystyle \ sol (1 {,} 33 \ cdot 10 ^ {- 16} \ sağ) ^ {\ circ}}$${\ görüntü stili F}$${\ displaystyle {\ üst çizgi {AT}},}$

${\ displaystyle F = 2 \ cdot \ sin \ sol ({\ frac {\ sol (1 {,} 33 \ cdot 10 ^ {- 16} \ sağ)) ^ {\ circ}} {2}} \ sağ) = 0 {,} 0000000000000000232 \ ldots = 2 {,} 32 \ ldots \ cdot 10 ^ {- 18} \; [\ matematik {LE}]}$

Açıkça: Açılı bacakların uzunluğu 1 milyar km'ye eşit olsaydı  ( ışık bu mesafe için yaklaşık 39 güne ihtiyaç duyardı), tendonun mutlak hatası yaklaşık 2.32 mm olurdu . ${\ görüntü stili {\ üst çizgi {AT}}}$

Uygulamalar

Bir kübik denklem gerçek katsayılı pergel, cetvel bir çift ve üç gerçek çözümler vardır, ancak ve ancak bir açısal üç parter (yani çözümleri inşa edilir) ile geometrik olarak çözülebilir. Polinomun katsayıları verildiği gibi alınır ve yapıda kullanılır. Özellikle, küpü ikiye katlarken gerekli olan 2'nin küp kökü bu araçlar kullanılarak oluşturulamaz, çünkü denklemin yalnızca gerçek çözümleri yoktur.${\ displaystyle x ^ {3} -2 = 0}$

Bir düzgün poligon ile yanlar, bir cetvel ile yapılabilir çifti pergel ve açılı üç Parteri durumunda ve sadece , farklı Fermat'ın asal sayılar formu 3'ten büyük , bakınız, aynı zamanda Pierpont asal sayı . ${\ görüntü stili n}$${\ displaystyle n = 2 ^ {r} 3 ^ {s} p_ {1} \ cdots p_ {k}}$ ${\ görüntü stili p_ {j}}$${\ displaystyle p_ {j} = 2 ^ {t} 3 ^ {u} +1}$

Heptagonun kübik denklemi yardımıyla aşağıdaki örnek, ek bir araç (örneğin tomahawk) yardımıyla üçe bölünebilen açının kosinüsünün nasıl bulunabileceğini açıklar.

Yedigen kübik denkleme sahiptir

${\ displaystyle (1) \; \; X ^ {3} + X ^ {2} -2X-1 = 0.}$

Sonuçları bir çözüm olarak ayarlarsanız${\ displaystyle X = {\ tfrac {\ sol (Y-1 \ sağ)} {3}},}$${\ displaystyle 1 + 6 \ cdot \ cos ({\ tfrac {2 \ pi} {7}})}$ ${\ görüntü stili (= 1 + 3 \ eta)}$

${\ görüntü stili (2) \; \; Y ^ {3} -21Y-7 = 0.}$

sokarak

${\ displaystyle Y = {\ sqrt {28}} \ cdot \ cos (\ teta)}$

basitleştirir

${\ displaystyle 7 \ cdot {\ sqrt {28}} \ sol (4 \ cdot \ cos ^ {3} (\ teta) -3 \ cdot \ cos (\ teta) \ sağ) = 7;}$

sonunda açının kosinüsünü elde ederiz, bu da üçe bölünebilir:

${\ displaystyle \ cos (3 \ teta) = {\ frac {1} {\ sqrt {28}}}}$.

Aşağıda, kübik denklemin bir yedigen örneğine nasıl dayandığı açıklanmaktadır.

${\ displaystyle (1) \; \; X ^ {3} + X ^ {2} -2X-1 = 0}$

belirlendi. Düzenli bir yedigen çizerek başlar.

İnşaat açıklaması

1. Bir Kartezyen koordinat sisteminin sıfır noktası etrafında yarıçapı olan yedigenin çevresi .${\ görüntü stili r = 6}$${\ görüntü stili O}$
2. noktaları işaretleyin ve${\ görüntü stili A (6 | 0), P (-1 | 0), Q (-3 | 0)}$${\ görüntü stili R (3 | 0).}$
3. Bir yarıçap ile bir yay haline kesim ekseni ve çizgi bir çapa sahip bir eşkenar üçgen tarafı${\ görüntü stili {\ üst çizgi {RQ}}}$${\ görüntü stili y}$${\ displaystyle K (0 | {\ sqrt {27}})}$${\ displaystyle L (0 | - {\ sqrt {27}});}$${\ displaystyle {\ üst çizgi {KL}}}$${\ görüntü stili {\ üst çizgi {RQ}}.}$
4. Nokta bağlantısı ile ve ile açılı tekabül${\ görüntü stili P}$${\ görüntü stili K}$${\ görüntü stili P}$${\ görüntü stili L;}$${\ görüntü stili \ açı {APK}}$${\ görüntü stili 3 \ teta.}$
5. Yarıçap ile etrafında yay${\ görüntü stili P}$${\ displaystyle {\ üst çizgi {PK}}.}$
6. z kullanarak açıyı üçe bölün . B. tomahawk, kesişme noktasını verir${\ displaystyle 3 \ teta,}$${\ görüntü stili S.}$
7. Paralel olarak yoluyla kesişme noktalarında sonuçları ve ve (gösterilmemiş olan) normal heptagon köşe noktaları${\ displaystyle {\ üst çizgi {KL}}}$${\ görüntü stili S}$${\ görüntü stili B, T}$${\ görüntü stili G;}$ ${\ görüntü stili B}$${\ görüntü stili G}$${\ görüntü stili ABCDEFG.}$

İnşaat kanıtı

Olsun hattının kesişme ile ekseni. İnşaat bunu gösteriyor${\ görüntü stili U}$${\ displaystyle {\ üst çizgi {ST}}}$${\ görüntü stili x}$

${\ displaystyle {\ overline {PK}} = {\ sqrt {28}}, \; \; \ cos \ sol (\ açı {APK} \ sağ) = {\ frac {1} {\ sqrt {28}} }, \; \; {\ üst çizgi {PU}} = {\ sqrt {28}} \ cdot \ cos \ sol (\ açı {APS} \ sağ) = {\ sqrt {28}} \ cdot \ cos \ sol ({\ frac {1} {3}} \ açı {APK} \ sağ).}$

İnşaat doğru ise

${\ displaystyle {\ overline {OU}} = 6 \ cdot \ cos \ sol ({\ frac {2 \ pi} {7}} \ sağ);}$  veya eşdeğer ise  ${\ displaystyle {\ overline {PU}} = 1 + 6 \ cdot \ cos \ sol ({\ frac {2 \ pi} {7}} \ sağ),}$

burada kosinüsün faktör tarafından normalleştirilmesi yarıçapın seçiminden kaynaklanır . Bu nedenle, yalnızca aşağıdaki kimliği belirlemeniz gerekir: ${\ görüntü stili 6}$${\ görüntü stili r = 6}$

${\ displaystyle {\ sqrt {28}} \ cdot \ cos \ sol ({\ frac {1} {3}} \ arccos \ sol ({\ frac {1} {\ sqrt {28}}} \ sağ) \ sağ) = 1 + 6 \ cdot \ cos \ sol ({\ frac {2 \ pi} {7}} \ sağ).}$

Bunu yapmak için, ol

${\ displaystyle \ xi = \ cos \ sol ({\ frac {2 \ pi} {7}} \ sağ) + i \ cdot \ sin \ sol ({\ frac {2 \ pi} {7}} \ sağ) }$

Bir ilk yedinci birlik kök bölgesindeki . Otur ${\ displaystyle \ matematik {C}}$

${\ displaystyle \ eta = \ xi + \ xi ^ {- 1} = 2 \ cdot \ cos \ sol ({\ frac {2 \ pi} {7}} \ sağ),}$

sonra

${\ displaystyle \ eta ^ {3} + \ eta ^ {2} -2 \ eta -1 = \ xi ^ {3} + \ xi ^ {2} + \ xi +1+ \ xi ^ {- 1} + \ xi ^ {- 2} + \ xi ^ {- 3} = 0.}$

Böylece kübik denklemin bir kökü ${\ görüntü stili \ eta}$

${\ displaystyle (1) \; \; X ^ {3} + X ^ {2} -2X-1 = 0.}$

Yukarıda açıklandığı gibi, bu açının kosinüsünü verir : ${\ görüntü stili 3 \ teta}$

${\ displaystyle \ cos (3 \ teta) = {\ frac {1} {\ sqrt {28}}}.}$

Morley teoremi

İlk başta Morley teoremi herhangi bir açının üçe bölünmesi için uygun gibi görünse bile, durum böyle değildir.

Belirli bir üçgende , köşelerdeki açılar ve ilk önce üçe bölünür. Bu, ek bir araç gerektirir, örn. B. bir dinamik geometri yazılımı (DGS) . Hassas bir şekilde oluşturulan üç -part açılar (kırmızı) köşe noktaları sağlamak , ve Morley üçgeni. ${\ görüntü stili ABC}$${\ görüntü stili A, B}$${\ görüntü stili C}$${\ görüntü stili D}$${\ görüntü stili E}$${\ görüntü stili F}$

Morley Teoremi:

Edebiyat

• Ernst-Erich Doberkat: Açının üçlü bölümü. İçinde: Die Drei (s. 59–85), Springer Verlag, 2019.
• Underwood Dudley : Trisektörler. Amerika Matematik Derneği, 1996.
• Underwood Dudley: Bir üçleme bütçesi. Springer Verlag, 1987.
• Christoph Scriba , Peter Schreiber : 5000 yıllık geometri. Springer Verlag, 2010.

İnternet linkleri

• Eric W. Weisstein : Açı Üçlemesi . İçinde: MathWorld (İngilizce).
• Jim Loy: Bir Açı ait Üç Bölümlü ( Memento 1 Ocak 2014 den Internet Archive )
• Matroids Matematik Gezegeni: Triseksiyon ve Haga Teoremi.
• İsviçre televizyonu: Origami çözülemeyen sorunları çözüyor. Einstein , 9 Nisan 2009.
• Sarah Kuchar : Açının üçe bölünmesi - zamanda bir yolculuk. 10 Ocak 2016.

Bireysel kanıt

1. ↑ Jürgen Köller: Yapılabilir üç bölmeli. Üçlü açı. 2009, 23 Nisan 2021'de erişildi . 
2. ↑ Johann Cigler : 1. Galois teorisinin ana maddesi. Katılar - halkalar - denklemler. İçinde: univie.ac.at. Viyana Üniversitesi, 26 Mart 2021'de erişildi . 
3. ↑ ^{a b c} Christoph Scriba , Peter Schreiber : 5000 yıllık geometri. Springer, 2010, s. 44.
4. ↑ Markus Asper: 1. Başlangıçlar: Milet'ten Atina'ya. (PDF) Matematik, ortam, metin. Erken Yunan matematiği ve çevresi. Sudhoff'un arşivi. Journal for the History of Science, 2003, s. 13 , erişim tarihi 13 Nisan 2021 . 
5. ↑ A. Jackter: Matematik Tarihi. İçinde: Antik Çağda Açı Üçlemesi Problemi. Rutgers University Press, 2000, 27 Kasım 2020'de erişildi . 
6. ↑ Christoph Scriba, Peter Schreiber: 5000 yıllık geometri. Springer, 2010, s. 78.
7. ↑ ^{a b} Horst Hischer : Quadratrix ve trisectrix arasında 1 bağlantı. (PDF) Didaktik Bir Yön Olarak Matematik Tarihi (2). Klasik problemlerin çözümü. İçinde: horst.hischer.de. 1994, s. 279 , erişim tarihi 31 Mart 2021 . 
8. ↑ Christoph Scriba, Peter Schreiber: 5000 yıllık geometri. Springer, 2010, s. 70.
9. ↑ K. Madde: Açının üç kesiti üzerinde → Şekil B. İçinde: Thurgau Doğa Araştırmaları Derneği'nden İletişimler . kaset 25 , 1902, s. 22. ff . ([ Çevrimiçi üzerine ZOBODAT Online'da] [PDF; erişilen 1 Nisan 2021]). 
10. ↑ Christoph Scriba, Peter Schreiber: 5000 yıllık geometri. Springer, 2010, s. 46.
11. ↑ K. Madde: Açının üçe bölünmesi hakkında, → bkz. son paragraf . İçinde: Thurgau Doğa Araştırmaları Derneği'nden İletişimler . kaset 25 , 1902, s. 22 ([ çevrimiçi üzerine ZOBODAT [PDF; 1 Nisan 2021 erişilen] Çevrimiçi]). 
12. ↑ Christoph Scriba, Peter Schreiber: 5000 yıllık geometri. Springer, 2010, s. 77.
13. ↑ ^{a b c} Dietmar Herrmann: Antik matematik. Yunan matematiğinin tarihi, sorunları ve çözümleri, Springer-Verlag, 2013, s. 155, nokta 3. ( Google kitap aramasında sınırlı önizleme ), 21 Ağustos 2020'de erişildi.
14. ^ ^{A b} Robert C. Yates: TRİSECTION PROBLEM, 3. Hiperbol. İçinde: ERIC. National Council of Teachers of Mathematics, Inc., Washington, DC, 1971, s. 32-33 , erişim tarihi 31 Mart 2021 . 
15. ↑ Katharina Wieser: 5.2.6. Hiperbolik nevrozlu Arap matematikçiler. Antik çağın üç klasik matematik problemi: küp ikiye katlama, açısal üçe bölme ve dairesel kareleme. Johannes Kepler University Linz, Mart 2013, s. 58 , 7 Nisan 2021'de erişildi . 
16. ↑ Katharina Wieser: 5.2.6. Hiperbolik nevrozlu Arap matematikçiler. Antik çağın üç klasik matematik problemi: küp ikiye katlama, açısal üçe bölme ve dairesel kareleme. Johannes Kepler University Linz, Mart 2013, s. 59 , 7 Nisan 2021'de erişildi . 
17. ↑ Christoph Scriba, Peter Schreiber: 5000 yıllık geometri. Springer, 2010, s. 179.
18. ↑ Christoph Scriba, Peter Schreiber: 5000 yıllık geometri. Springer, 2010, s.180.
19. ↑ F. Vogel: Bir açının üçlü bölümü için yaklaşık yapılar hakkında. dergi f. matematik ve doğa bilimleri Eğitim, 62. yıl, 1931, s. 145–155.
20. ↑ ^{a b} Karl Hunrath: Albrecht Dürer'in bir yayın yaklaşık üçlü bölümü. Bibliotheca Mathematica. Matematik Bilimleri Tarihi Dergisi. Heidelberg Üniversitesi, 1906, s. 120 , erişim tarihi 12 Nisan 2021 . 
21. ↑ Christoph Scriba, Peter Schreiber: 5000 yıllık geometri. Springer, 2010, s. 283.
22. ↑ Jesper Lützen: Wantzel neden bir asırdır göz ardı edildi? İmkansızlık sonucunun değişen önemi. Historia Mathematica 36, ​​​​2009, s. 387.
23. ↑ Christoph J. Scriba, Peter Schreiber: 5000 yıllık geometri. Springer-Verlag, Üçüncü Baskı, 2010, s. 405.
24. ↑ ^{Bir b} Pierre Wantzel : Recherches sur les moyens de reconnaitre si un Problème de Géométrie peut se résoudre avec la règle et le compas (=  Journal de Mathématiques pures et Appliquees (Liouville Dergisi) . Cilt 2 ). 1837, s. 366-372 ( PDF ). 
25. ↑ Craig Smorynski: Matematik Tarihi: Bir Ek . Springer, 2007, ISBN 978-0-387-75480-2 , s. 130 ( Google Kitaplar ).  Wantzel'in Ruffini ve Abel'ın daha önceki çalışmasındaki kanıtlarının tarihsel sınıflandırması ve Galois ile zamansal bir karşılaştırma için.
26. ↑ Jesper Lützen: Wantzel neden bir asırdır göz ardı edildi? İmkansızlık sonucunun değişen önemi. Historia Mathematica 36, ​​​​2009, s. 378-379.
27. ↑ Jesper Lützen: Wantzel neden bir asırdır göz ardı edildi? İmkansızlık sonucunun değişen önemi. Historia Mathematica 36, ​​​​2009, s. 379.
28. ↑ Jesper Lützen: Wantzel neden bir asırdır göz ardı edildi? İmkansızlık sonucunun değişen önemi. Historia Mathematica 36, ​​​​2009, s. 391.
29. ↑ Hans Humenberger : Deliç problemi ve üç boyutlu bölme üzerine temel matematiksel düşünceler . İçinde: Uluslararası. Matematik Haber No. 219, 25-43 . 2012, s. 38–40 ( çevrimiçi [PDF; erişim tarihi: 14 Kasım 2020]). 
30. ↑ ^{a b} Falko Lorenz : Cebir Cilt I: Alanlar ve Galois Teorisi. Springer, s. 52.
31. ↑ K. Robin McLean: cetvel ve pergel ile açıları üçe bölme. Matematik Gazetesi. 92, s. 320-323.
32. ^ Underwood Dudley : Trisektör geldiğinde ne yapmalı. Missouri Bilim ve Teknoloji Üniversitesi, 1983, erişim tarihi 21 Kasım 2020 .  Ayrıca bkz. Mathematical Intelligencer , Cilt 5, 1983, No. 1 ve bununla ilgili kitabında.
33. ↑ Hans Humenberger: İşaretli bir cetvel ve kağıt katlamalar (origami) kullanan 8 yapı. Delic problemi ve açıların üç boyutlu bölümü üzerine temel matematiksel düşünceler. Viyana Üniversitesi, 2012, s. 41–42 , 13 Nisan 2021'de erişildi . 
34. ↑ Bodo v. Pape: 7.4 Tomahawk ile üçlü. İçinde: Makro Matematik. Cebir ve Analizin Ötesinde: Algoritmalar. BoD - Talep Üzerine Kitaplar, 2016, ISBN 373579419X ( Google Kitap Arama'da sınırlı önizleme )
35. ↑ ^{a b c d} Ludwig Bieberbach : Kübik yapıların öğretimi üzerine, saf ve uygulamalı matematik dergisi. H. Hasse ve L. Schlesinger, Cilt 167, Walter de Gruyter, Berlin 1932, s. 142–146 , DigiZeitschriften , sayfa 143'te karşılık gelen formüller ve 144 sayfa 144 görüntü, 6 Haziran 2018'de erişildi.
36. ↑ K. Madde: Açının üçe bölünmesine . İçinde: Thurgau Doğa Araştırmaları Derneği'nden İletişimler . kaset 25 , 1902, s. 20 ([ çevrimiçi üzerine ZOBODAT Çevrimiçi] [PDF; 27 Mart erişilen, 2021]). 
37. ↑ K. Madde: Açının üçe bölünmesine . İçinde: Thurgau Doğa Araştırmaları Derneği'nden İletişimler . kaset 25 , 1902, s. 21 ff . ([ Çevrimiçi üzerine ZOBODAT Çevrimiçi] [PDF; 24 Mart'ta erişilen, 2021]). 
38. ↑ K. Madde: Açının üçe bölünmesine . → Şek.a. Bir hiperbol yardımıyla bir açının üçe bölünmesi. İçinde: Thurgau Doğa Araştırmaları Derneği'nden İletişimler . kaset 25 , 1902 ([ çevrimiçi üzerine ZOBODAT Online] [PDF; 2020 Temmuz 29 erişilen]). 
39. ↑ Justin Seago : Maclaurin Trisectrix. CR College of the Redwoods, 8 Aralık 2008, 1 Eylül 2020'de erişildi . 
40. ↑ Matthias Sebastian Konzett: 3.5.1.Origami kullanarak çözüm. İmkansız imkanlı? Viyana Üniversitesi, 3 Eylül 2012, sayfa 46 ve devamı , Erişim tarihi 23 Kasım 2020 . 
41. ^ ^{A b} Greg Blonder: Açıyı bir cetvelle üçe bölme. + artı. dergisi, 9 Nisan 2021'de erişildi . 
42. ↑ Albrecht Dürer: Zirckel ve Richtscheyt ile ölçümün altını çizin, çizgilerde seviye ve tüm corpora. Bavyera Eyalet Kütüphanesi, Dijital Koleksiyonlar, 1525, erişim tarihi 12 Nisan 2021 . 
43. ↑ Karl Hunrath: Albrecht Durer bir yayın yaklaşık üç katlı bölümü. Bibliotheca Mathematica. Matematik Bilimleri Tarihi Dergisi. Heidelberg Üniversitesi, 1906, s. 121 , 11 Nisan 2021'de erişildi . 
44. ↑ Karl Hunrath: Albrecht Durer bir yayın yaklaşık üç katlı bölümü. Bibliotheca Mathematica. Matematik Bilimleri Tarihi Dergisi. University of Heidelberg, 1906, s.122 ff. , Erişim tarihi: 11 Nisan 2021 . 
45. ↑ Jim Loy: Bir Açının Üçgen Kesimi. Analoji yapmak için: (son paragraf). İçinde: jimloy.com. Arşivlenmiş orijinal üzerinde 25 Şubat 2012 ; 27 Mart 2021'de erişildi (İngilizce). 
46. ↑ ^{a b c} Rouben Rostamian: Bir açı üçlemesi. Maryland Üniversitesi, Baltimore County, 23 Mart 2011, erişim tarihi 3 Şubat 2020 . 
47. ↑ Andrew M. Gleason : Açı Üçlemesi, Heptagon ve Triskaidecadon. The American Mathematical Monthly, Cilt 95, Sayı 3, sayfa 190.
48. ↑ Andrew M. Gleason: Açı Üçlemesi, Heptagon ve Triskaidecadon. The American Mathematical Monthly, Cilt 95, Sayı 3, sayfa 191.
49. ↑ Andrew M. Gleason: Açı Üçlemesi, Heptagon ve Triskaidecagon. (PDF) The American Mathematical Monthly. Florida Atlantic University, Mart 1988, s. 187 , 6 Nisan 2021'de erişildi . 
50. ^ ^{Bir b c} Andrew M. Gleason: Açı Üçlü, yedigen, ve Triskaidecagon. (PDF) The American Mathematical Monthly. Florida Atlantic University, Mart 1988, s. 186 , 6 Nisan 2021'de erişildi . 
51. ↑ Horst Hischer: 1.1.2 Uygulama ve oyun arasındaki Morley üçgeni. Matematiğin temel terimleri: Kökeni ve gelişimi: yapı - fonksiyon - sayı. Springer-Verlag, 13 Haziran 2012, sayfa 2-4 , 5 Nisan 2021'de erişildi .