Bir tensör a, çoklu doğrusal eşleme haritalar belirli sayıda vektörleri bir vektör üzerine olan ve yerine bir evrensel özellik . Diferansiyel geometri de dahil olmak üzere birçok alanda kullanılan lineer cebirden matematiksel bir nesnedir ve lineer haritalama kavramını genişletir. Terim başlangıçta fizikte tanıtıldı ve ancak daha sonra matematiksel olarak daha kesin hale getirildi.
Diferansiyel geometri ve fiziksel disiplinlerde, lineer cebir anlamındaki tensörler genellikle dikkate alınmaz, daha ziyade basitlik için tensörler olarak da adlandırılan tensör alanları ile ilgilenilir. Bir tensör alanı, uzaydaki her noktaya bir tensör atayan bir haritadır. Birçok fiziksel alan teorisi, tensör alanlarıyla ilgilenir. En belirgin örnek genel göreliliktir . Tensör alanlarının araştırılmasıyla ilgilenen matematiksel alt alana tensör analizi denir ve fiziksel ve mühendislik disiplinlerinde önemli bir araçtır.
Konsept geçmişi
Tensör kelimesi ( Latince ihale ' to span'dan gelen geçmiş ortaçtan türetilmiştir ) matematiğe 1840'larda William Rowan Hamilton tarafından tanıtıldı; onu kuaterniyonlarının mutlak değerini belirtmek için kullandı , yani modern anlamda bir tensör değil. James Clerk Maxwell çağrıda görünmüyor stres tensörünü diye transfer, elastisite teorisi için elektrodinamik , kendini.
Modern anlamında, skaler , vektör , matrisin bir genellemesi olarak tensör kelimesi ilk olarak Woldemar Voigt tarafından kristallerin temel fiziksel özellikleri elementer temsilde (Leipzig, 1898) kitabında tanıtıldı .
Mutlak diferansiyel geometri başlığı altında , Gregorio Ricci-Curbastro ve öğrencisi Tullio Levi-Civita , 1890 civarında Riemann manifoldları üzerinde tensör hesabını geliştirdi . Sonuçlarını 1900'de , kısa süre sonra başka dillere çevrilen ve Albert Einstein'ın genel görelilik kuramını formüle etmek için ihtiyaç duyduğu matematiksel temelleri edindiği Calcolo diferenziale assoluto kitabıyla daha geniş bir uzman kitleye sundular . Einstein , 1916'da tensör analizi terimini kendisi icat etti ve teorisiyle tensör hesabının popülerleşmesine önemli bir katkı yaptı; Ayrıca Einstein'ın toplam sembollerini atlayarak çift indekslerin eklendiği toplamlar kuralını tanıttı .
Tensör türleri
Sonlu boyutlu bir vektör uzayından başlayarak, skalerlere tip tensörler , sütun vektörlerine tip tensörler ve kovektörlere (veya satır vektörleri) tip tensörler denir . Daha yüksek seviyeli tensörler, argümanlar ve harita değerleri olarak daha düşük seviyeli tensörler ile çok doğrusal eşlemeler olarak tanımlanır . Örneğin, tip bir tensör bir şekilde anlaşılabilir vektör uzayı arasında ya da bir doğrusal haritalama çift doğrusal haritalama bir vektör ile ve bağımsız değişken olarak bir covector.




Örneğin, fizikteki mekanik gerilim tensörü ikinci dereceden bir tensördür - bir sayı ( stresin gücü ) veya bir vektör (bir ana gerilim yönü ) bir cismin gerilim durumunu tanımlamak için her zaman yeterli değildir . Türünde bir tensör olarak kabul edildiğinde , üzerine etki eden kuvveti (bir kovektör olarak) bir yüzey elemanına (vektör olarak) atayan doğrusal bir haritalama veya yer değiştirme sırasında meydana gelen işi atayan çift doğrusal bir haritalamadır. yüzey alanı bir yüzey elemanına ve bir yer değiştirme vektörüne etki eden voltajın etkisi gerçekleştirilir.

Sabit bir vektör uzayı temeli ile ilgili olarak , farklı tensör türlerinin aşağıdaki temsilleri elde edilir:
- Tek bir sayı ile bir skaler
- Bir sütun vektörüne göre bir vektör
- Bir çizgi vektörüne göre bir yardımcı vektör
- Bir matris aracılığıyla ikinci dereceden bir tensör
Gerilme tensörünün bir yüzey elemanına uygulanması daha sonra z'dir. B. Sütun vektörlü bir matrisin çarpımı ile verilir. Daha yüksek mertebeden tensörlerin koordinatları, daha yüksek boyutlu bir şemada buna göre düzenlenebilir. Bir sütun vektörünün veya matrisinkilerden farklı olarak, bir tensörün bu bileşenleri bir veya ikiden fazla indekse sahip olabilir. Argüman olarak üç vektör des içeren üçüncü dereceden bir tensör örneği , bu matrisin sütunlarının bir fonksiyonu olarak 3 x 3 matrisin determinantıdır. Bir ortonormal tabana göre, Levi-Civita sembolü ile temsil edilir .


Vektörlerin eş ve kontravaryansı
Terimleri ko ve kontravaryant bakınız koordinat temsilleri vektörlerinin lineer formları daha sonra makalede anlatıldığı gibi, ve, aynı zamanda tensörlerle uygulanır. Bu tür koordinat temsillerinin, temeldeki vektör uzayındaki bir taban değişikliğine göre nasıl davrandığını tanımlarlar.
Eğer bir -boyutlu vektör uzayında bir taban tanımlıyorsa , o zaman bu uzayın her vektörü, bir sayı demeti -koordinatları- kullanılarak temsil edilebilir . Koordinat gösterimi farklı bir temele dayanıyorsa, koordinatlar (bir ve aynı vektör) bu yeni temele göre değişecektir. Bu nedenle, farklı bir temele geçiş, koordinat gösteriminin bir dönüşümünü gerektirir. Aşağıdakiler geçerlidir: Yeni taban eski tabanda belirlenirse , yeni koordinatlar şurada karşılaştırılarak elde edilir:









Bu yüzden:

Üç boyutlu bir Öklid uzayında bir döner bir ortogonal baz, örneğin, yaklaşık -Axis, vektörleri koordinat koordinat alanında da döndürme çevresinde etrafında, yani, -Axis, fakat ters yönde varılabilmektedir . Temel dönüşümün karşısındaki bu dönüşüm davranışına kontravariant denir . Genellikle, gösterimi kısaltan vektörler, koordinat vektörleriyle tanımlanır, böylece vektörlere genellikle karşı değişken olarak atıfta bulunulur.






Öte yandan bir doğrusal form veya bir kovector , vektör uzayı üzerinde skaler değerli bir doğrusal eşlemedir . Değerlerini vektörler bazında koordinatlar olarak atayabilirsiniz ,,. Doğrusal bir formun koordinat vektörleri, temel tuple gibi aşağıdaki gibi dönüşür:




bu nedenle bu dönüşüm davranışı kovaryant olarak adlandırılır. Doğrusal formlar koordinat vektörleriyle yeniden tanımlanırsa, genellikle doğrusal formlar da kovaryant olarak belirlenir. Vektörlerde olduğu gibi, altta yatan temel bağlamdan ortaya çıkar. Bu bağlamda ikili vektörlerden de söz edilir.
Bu isimler tensörlere aktarılır. Bu, tensörlerin tanımıyla ilgili bir sonraki bölümde açıklanmıştır .

tanım
( r , s ) -tensör uzayı
Aşağıda, tüm vektör uzayları gövde üzerinde sonlu boyutludur . İle tüm kümesine çağrısı doğrusal formları gelen vektör uzayda içinde vücutta daha genel - - ve tüm kümesi a -linear görüntüleri -Vektorraums bir de vektör alanı . Are üzerinde vektör uzayları , gitme vektör uzayı çok lineer formlar ile belirlenmiş. Tümü - çok doğrusal eşlemeler kümesini , burada özellikle -kat -doğrusal eşlemeleri karşılık gelecek şekilde belirtin . Durumunda ve , şekiller iki çizgili vardır .






















Eğer bir - vektör uzayı denir onun ikili alanı . Sonra ( evrensel özelliğe göre ) kanonik izomorfizmler var.



ve daha genel

Kanonik izomorfizm bir vektör alan onun ile çift boşluk (değiştirerek aşağıdaki göre ve bu yüzden göre göre bu) izomorf için tensör ürün . ( Bu bölümde daha sık kullanılan kanonik tanımlamanın yanı sıra, tensör çarpım uzayının bir çok-doğrusal formlar uzayı olarak gerçekleştirilmesi için , evrensel özellik ve tensör ürünleri ve çok-doğrusal biçimler bölümlerine bakınız .)










Orada doğal izomorfizmler aşağıdaki tip:

Bu doğal izomorfizmler azaltılması dayanmaktadır için kat doğrusal dönüşümler kat doğrusal eşlemeler (bakınız Currying veya Schönfinkeln bir yandan ve ilgili) evrensel özellik tensör ürünün diğer yandan - bir çok kez kullanılması:



Yukarıda öne sürülen doğal izomorfizm,
özellikle
![{\ displaystyle {\ {matrix} L ^ {k} (E_ {1}, \ dotsc, E_ {k}; K) & {\ stackrel {\ sim} {\ longrightarrow}} & L (E_ {1} \ otimes \ dotsc \ otimes E_ {m}; E_ {m + 1} ^ {*} \ otimes \ dotsc \ otimes E_ {k} ^ {*}) \\\ lambda & \ longmapsto & \ sol [\ lambda _ { (1, \ dotsc, m)} \ kolon v_ {1} \ otimes \ dotsc \ otimes v_ {m} \ mapto \ lambda _ {(v_ {1}, \ dotsc, v_ {m})} \ in ( E_ {m + 1} \ bazen \ nokta \ bazen E_ {k}) ^ {*} \ sağ] {\ metin {,}} \\ && {\ metin {nerede}} \ sol [\ lambda _ {(v_) { 1}, \ dotsc, v_ {m})} \ iki nokta üst üste (v_ {m + 1} \ otimes \ dotsc \ otimes v_ {k}) \ mapto \ lambda (v_ {1}, \ dotsc, v_ {k} ) \ sağ] \\\ bitiş {matris}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5af0ca5982fcea7f59fe2aa8996dd0c3de44ce0)
ve tanımlama lineer form için yapılır. Burada
temel tensörler üzerindeki eşlemeleri ( tensör ürününün bir elemanı olarak Tensör bölümüne de bakınız ) temel gövde üzerinde bir üretici sistem olarak tanımlamak yeterlidir . Vakalarda ve temel gövde ile tanımlanabilen boş tensör ürününün ortaya çıktığını eklemek gerekir. Özellikle, vektör uzayları ve tanımlama
için bu nedenle








-
 .
.
Tanım: İkili uzaylı bir cisim üzerinde sabit bir vektör uzayı için, şu şekilde tanımlansın:





ile gelen girdileri ve gelen girişleri . Bu kümenin elemanlarına
tensörler, seviyenin kontravaryantı ve seviyenin kovaryantı denir . Kısacası, tensör tipinden bahsediliyor . Toplamı denir seviyesi veya sıralaması tensörü.







Yukarıdaki düşüncelerle (için ve yanı sıra için ve için ) genel sonuç şudur:







Böylece, türdeki tensörlerin vektör uzayı ,
tensör çarpımını , yani yukarıdaki kanonik tanımlama yoluyla gerçekleştirir.



-
 .
.
Bu doğal izomorfizmler bir anlamına da
indüktif seviyesinin tansörlerine tanımlamak olarak çoklu doğrusal dönüşümler daha düşük düzeyde tensör boşluklar arasında. Belirli bir tipte bir tensör için birkaç eşdeğer olasılık vardır.

Fizikte vektör uzayları genellikle aynı değildir, örn. B. Bir hız vektörü ve bir kuvvet vektörü eklenemez. Ancak, yönleri birbiriyle karşılaştırabilir, i. yani, vektör uzaylarını skaler faktör dışında birbirleriyle tanımlayın. Dolayısıyla tip tensörlerin tanımı buna göre uygulanabilir. Fizikte (boyutlu) skalerlerin tek boyutlu vektör uzaylarının elemanları olduğu ve
skaler çarpımı olan vektör uzaylarının ikili uzayları ile tanımlanabileceği de belirtilmelidir. Biri z çalışır. B. kuvvet vektörleri ile, ancak skaler çarpım kullanılmayan kuvvetler kovektör olarak kabul edilmelidir.

Harici tensör ürünü
Bir (dış) tensör çarpımı veya
tensör çarpımı , iki tensör arasındaki bir bağlantıdır . Izin bir vektör alanı ve olmak ve tansörler. (dış) tensör ürünü ve içinden
geçen tensördür








tanımlanmış. İşte bunlar ve bunlar .


( r , s ) -tensör örnekleri
Aşağıda, sonlu boyutlu vektör uzayları olsun ve olsun .


- (0,0) -tensörler kümesi, alttaki gövde ile izomorfiktir . Herhangi bir doğrusal şekle veya vektöre bir gövde öğesi atamazsınız. Bu nedenle (0,0) -tensörler olarak atama.

- (0.1) -tensörler herhangi bir lineer formu ve bir vektörü bir sayıya göre düzenler, böylece üzerindeki lineer formlara karşılık gelir .


- (1,0) tensörler, bir vektöre değil, doğrusal bir forma bir sayı atar. Dolayısıyla bunlar, çift yönlü vektör uzayının elemanlarıdır . Sonlu boyutlu vektör uzayları durumunda, burada aşağıdakiler geçerli olduğundan (bkz. izomorfizm ) ilk vektör uzaylarına karşılık gelirler .



- Bir doğrusal eşleme sonlu boyutlu vektör alanlar arasındaki bir unsuru olarak anlaşılabilir ve daha sonra bir (1,1) -tensor olup.


- Bir çift doğrusal form , bir (0,2) -tensörünün bir öğesi olarak anlaşılabilir . Özellikle, skaler ürünler (0.2) tensörler olarak anlaşılabilir .


- Kronecker'in ö tekrar (0.2) tensör olup. Bu bir öğedir ve bu nedenle çok doğrusal bir eşlemedir . Çok doğrusal eşlemeler, temel vektörler üzerindeki etkiyle benzersiz bir şekilde belirlenir. Yani Kronecker Deltası açıkça




- kesinlikle.
- Belirleyici bir sütun alternatif çoklu doğrusal formu olarak yorumlanır matrisler, (n, 0) -tensor bir taslaktır. Bir ortonormal taban ile ilgili olarak, Levi-Civita sembolü ("epsilon tensörü") ile temsil edilir . Özellikle üç gerçek boyutta, determinant üçüncü dereceden bir tensördür ve ortonormal bir temelin elemanları için geçerlidir . Hem Kronecker delta hem de Levi-Civita sembolü, tensörlerin simetri özelliklerini incelemek için yaygın olarak kullanılır. İndeksler değiştirildiğinde Kronecker deltası simetriktir, Levi-Civita sembolü antisimetriktir, böylece tensörler onların yardımıyla simetrik ve antisimetrik parçalara bölünebilir.



- İkinci dereceden kovaryant tensöre başka bir örnek de eylemsizlik tensörüdür .
- Olarak elastik teori , bir genelleştirilmiş Hook denklemi de sokulmasıyla tensör analizi yardımıyla, esnek bir ortam içinde kuvvetler ve buna bağlı suşları ve bozulmaları arasındaki ilişki hakkında suşu tensörünün bozulmaları ve deformasyonlara tarif ve gerilme tensörü tarif etmektedir, deformasyonlara neden olan kuvvetlerdir. Ayrıca bkz . sürekli ortam mekaniği .
- Skaler çarpımı olan bir vektör uzayı olsun . Yukarıda bahsedildiği gibi, skaler ürün her iki argümanda da doğrusaldır, yani bir (0.2) -tensör veya iki katlı kovaryant tensör. Ayrıca bir metrik tensörden veya kısaca “metrik” ten bahsediliyor . Burada belirtilmelidir ki, kendisi bir metrik uzay anlamında bir metrik değildir, bir tane yaratır. Vektör alan bir tabana göre metrik koordinatları vardır ile gösterilmiştir; ve vektörlerin koordinatları olsun ve aynı tabana göre. Bu nedenle aşağıdakiler iki vektörün eşlenmesi için geçerlidir ve metriğin altındaki














- Eş ve karşı değişken tensörler arasındaki geçiş, metrik aracılığıyla geçirilebilir.

- sonuçlandırmak.
- Riemann manifoldları üzerindeki diferansiyel geometride bu metrik aynı zamanda konumun bir fonksiyonudur. Metrik tensör durumunda özellikle bir Riemann metriği durumunda , konumun tensör değerli bir işlevine tensör alanı adı verilir.
Temel
Temel ve boyut
Yukarıdaki gibi bir vektör uzayı olsun , o zaman uzaylar da vektör uzaylarıdır. Ayrıca, şimdi tabanı ile sonlu boyutlu olsun . İkili temel ile gösterilir. Tensörlerin uzayı da sonlu boyutludur ve







bu uzayın temelidir. Bu, her öğenin geçebileceği
anlamına gelir

temsil ediliyor. Bu vektör uzayının boyutu . Her sonlu boyutlu vektör uzayında olduğu gibi, tensörler uzayında da bir fonksiyonun temelde nasıl çalıştığını söylemek yeterlidir.

Yukarıdaki toplamlar gösterimi çok fazla evrak işi gerektirdiğinden, Einstein'ın toplamlar kuralı sıklıkla kullanılır. yani bu durumda yazarsın

Katsayılara , tabana göre tensörün bileşenleri denir . Genellikle tensörün bileşenleri tensörün kendisiyle tanımlanır. Bunun için fizikteki tensör temsillerine bakınız .


Taban değişikliği ve koordinat dönüşümü
Let ve olmak vektör uzayı farklı bazların çiftleri . Her temel vektör de dahil olmak üzere her vektör, temel vektörlerin doğrusal bir kombinasyonu olarak temsil edilebilir . Temel vektör şu şekilde temsil edilir:







Boyutlar , tabanlar arasındaki taban dönüşümünü belirler ve . Bu herkes için geçerli . Bu işleme baz değişikliği denir.




Ayrıca, tensörün bileşenleri tabana göre olsun . Denklem daha sonra tensör bileşenlerinin dönüşüm davranışı için sonuçlanır.




Kural olarak, tensörün koordinat gösterimi ile dönüşüm matrisi arasında bir ayrım yapılır . Dönüşüm matrisi , indekslenmiş bir niceliktir, ancak bir tensör değildir. Öklid uzayında bunlar rotasyon matrisleri ve özel görelilik z'dir. B. Dört boyutlu Minkowski uzayında "dönüşler" olarak da anlaşılabilen Lorentz dönüşümleri . Bu durumda, dört tensör ve dört vektörden söz edilir .



örnek
Bileşenlerin yardımıyla, bir tensör bir tabana göre temsil edilebilir. Örneğin, belirli bir temel sistemde sıra 2'ye sahip bir tensör aşağıdaki gibi bir matris olarak temsil edilebilir:



Bu , matris çarpımı yardımıyla değerin karşılık gelen temel sistem çerçevesinde hesaplanmasını sağlar :


Şimdi atalet tensörü özel olarak ele alınırsa , seçilen bir koordinat sistemine göre açısal hıza sahip katı bir cismin dönme enerjisini aşağıdaki gibi hesaplamak için kullanılabilir :




Tensörler üzerindeki işlemler
Tensör çarpımına ek olarak, (r, s) -tensörleri için başka önemli işlemler de vardır.
İç ürün
Bir vektörün (veya bir (eş-) vektörün ) bir tensörle iç çarpımı , (veya ) tensördür;






veya aracılığıyla

tanımlanmış. Bu, tensörün sabit bir vektör veya sabit bir kovektör üzerinde değerlendirildiği anlamına gelir .




Tensör koniği
Verilenler bir (r, s) -tensörü ve ve . Tensör koniği tensörü oluşturur




tensör üzerinde

uzak. Bu işleme tensör daralması veya iz oluşumu denir . (1,1) tensör durumunda, tensör koniği şuna karşılık gelir:

belirleme izini bir Endomorfizma.

Einstein'ın toplama kuralının yardımıyla, tensör daralması çok kısaca gösterilebilir. Örneğin, seçilen bir temele göre iki aşamalı tensörün katsayıları (veya koordinatları) olsun . Eğer biri bu (1,1) -tensörü daraltmak isterse, genellikle sadece katsayılar yerine yazılır . Einstein'ın toplama kuralı şimdi tüm özdeş indekslerin toplandığını ve dolayısıyla endomorfizmin izine karşılık gelen bir skaler olduğunu belirtiyor. Öte yandan ifadesi tanımlanmamıştır, çünkü aynı endeksler yalnızca biri üstte diğeri alttaysa toplanır. Öte yandan, birinci dereceden bir tensördür.







Geri çekme (dönüş nakliyesi)
Bir izomorfizm olması gerekmeyen vektör uzayları arasında doğrusal bir eşleme olsun . Dönüş nakliyesi, içinden geçen bir rakamdır .




tanımlanmış. var ve .


İlerletmek
Izin bir vektör uzayı izomorfizm . İleri itmek Define aracılığıyla ile




Orada , ve . İle olur taşıma geri doğrusal form listelenen. Somut olarak, bu , geri dönüş taşımasına benzer, ileri itme ile izomorfizminden vazgeçilebilir ve bu işlemi yalnızca tensörler için tanımlayabilir.








tensör cebiri
Izin bir vektör uzayı bir aşkın vücuda . Sonra bitti



Sözde tensör cebirini tanımlar. Tensör çarpımının homojen bileşenler üzerinde verdiği çarpma ile üniter bir çağrışımsal cebir olur .

Tensör ürün alanı
Bu bölümde tensör çarpım uzayları tanımlanır ve bunlar genellikle cebirde ele alınır . Bu tanım (r, s) -tensörlerinden daha geneldir, çünkü burada tensör uzayları farklı vektör uzaylarından oluşturulabilir.
İki faktörün tensör çarpımı için evrensel özellik
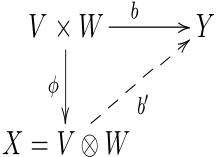
Tensör ürününün evrensel özelliği
Alan üzerinde Let ve vektör uzayları . Varsa ek vektör uzayları, herhangi bilineer haritalama ve doğrusal haritalama, daha sonra bağlantı da iki doğrusal haritalama. Bir çift doğrusal eşleme verilirse, ondan herhangi bir sayıda başka çift doğrusal eşleme oluşturulabilir. Tüm çift doğrusal haritaların bu şekilde (benzersiz bir şekilde) doğrusal haritalarla ilişkilendirilerek oluşturulabileceği bir çift doğrusal eşleme olup olmadığı sorusu ortaya çıkar . Böyle evrensel bir nesne, i. H. görüntü uzayını içeren çift doğrusal eşleme, and öğesinin tensör ürünü olarak adlandırılır .











Tanım: Vektör uzaylarının ve her vektör uzayının tensör çarpımı olarak adlandırılır, bunun için aşağıdaki evrensel özelliği karşılayan bir çift doğrusal eşleme vardır :





- Her çift doğrusal haritalama için bir vektör uzaya tam olarak bir doğrusal haritalama var hepsi için geçerlidir, böylece :






Böyle bir vektör uzayı varsa , izomorfizm dışında tek olarak belirlenir. Bilineer formlu (tensör ürünü olarak ) böyle bir ikinci vektör uzayı zaten varsa , o zaman özelliği ile benzersiz olarak belirlenmiş doğrusal eşleştirmenin yanı sıra , aynı zamanda evrensel özelliğe sahip olduğundan , özelliği ile benzersiz bir şekilde belirlenmiş doğrusal eşleştirme de vardır . Yani hem ve hem de izomorfizmdir. Biri yazıyor ve . Böylece evrensel özellik olarak yazılabilir. Bu tür ürün uzaylarının inşası için Tensor ürünü makalesine atıfta bulunulur .















Tensör ürününün evrensel özelliği, yukarıdaki soruya olumlu bir cevap verir ve aşağıdaki gibi formüle edilebilir:

surjective (varlık ifadesi) ve injective (teklik ifadesi), dolayısıyla bijective ve dolayısıyla vektör uzaylarının bir izomorfizmidir. Bu durumda tensör çarpım uzayının dual uzayı bilineer formların uzayı olarak yorumlanır. Daha önce bahsedilen tanımlamalarla birlikte, bu şu sonuçlara yol açar:

Tensör ürününün bir elemanı olarak tensör
Matematikte tensörler, tensör ürünlerinin elemanlarıdır.
Bu olsun bir gövde ve orada vektör uzayı vücut üzerinde .



Tensör ürünü bir a, olan elemanlar formun sembollerin toplamı olan vektör uzayı




NS. Bu semboller için aşağıdaki hesaplama kuralları geçerlidir:


Formun tensörlerine temel denir . Her tensör, temel tensörlerin toplamı olarak yazılabilir, ancak bu temsil, iki hesaplama kuralının ilkinden görülebileceği gibi, önemsiz durumlar dışında açık değildir.

Varsa , bir baz ve (için , ), daha sonra





bir temel boyutu , bu nedenle tek tek vektör boşlukların boyutları bir ürünü olduğu,


Birkaç faktöre genişletme: Çoklu tensör ürünleri ve çok doğrusal formlar için evrensel özellik
Önceki hususlar üzerinde evrensel özelliği aşağıdaki gibi çeşitli faktörlere kadar uzatılabilir.
Dual uzay arasında (evrensel özelliğine göre) kutu alanı ile tanımlanabilir arasında - çoklu doğrusal formları :



- Eğer bir doğrusal şeklidir üzerinde, daha sonra bir - bir çoklu doğrusal bir form kazandırır . Her çok-doğrusal formun bu şekilde oluşturulup oluşturulamayacağı sorusu ortaya çıkıyor . Olumlu cevap , tensör ürününün evrensel özelliğini verir :





- Tersine , eğer bir -Multlinearform ise, o zaman ona karşılık gelen lineer form - evrensel özelliğe göre - onu elementer tensörler için tanımlayarak (evrensel özelliğe uygun olarak) ve sonra onu lineer olarak tüm vektör uzayına genişleterek belirlenir . Evrensel özelliğe göre, temel tensörler için aşağıdakiler geçerlidir:





Yukarıda formüle edildiği gibi ( evrensel özellik bölümünde ), iki vektör uzayı durumunda , evrensel özellik aynı zamanda (izomorfizm dışında) birkaç faktör için de geçerlidir. Ve bu şu şekilde formüle edilebilir ve aynı zamanda yukarıdaki iki ayna noktasının ifadesini içerir:
Tanım: olmalı olsun hem de ve vücut üzerinde vektör uzayı . Daha sonra, aşağıdaki özelliğe sahipse , çok-doğrusal eşleme, üzerinde vektör uzaylarının tensör çarpımı olarak adlandırılır : Herhangi bir çok-doğrusal görüntüleme için, tüm demetler için özelliğe sahip benzersiz bir doğrusal harita vardır , ardından şöyle yazar:












Böyle bir çok doğrusal eşleme ile
böyle bir vektör uzayı varsa , o zaman vektör uzayı bu evrensel özellik nedeniyle izomorfizm dışında benzersiz olarak belirlenir. Bu nedenle, genellikle sadece vektör uzayından bahsediyoruz, ancak kesin olarak konuşursak, ilişkili çok doğrusal eşleme de tensör ürününün bir parçasıdır.




Aslında, böyle bir tensör ürünü , vektör uzayları kategorisi için oluşturulabilir (daha kesin olarak: verilen vektör uzayları üzerinde herhangi bir vektör uzayına çok doğrusal eşlemeler kategorisinde ) . İzomorfizm dışında evrensel özelliği ile açıkça karakterize edilir.
![{\ displaystyle \ psi: V_ {1} \ kez \ dotsb \ kez V_ {s} \ ila [??]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/597d0dd2574ad69e6b77499917be8e727960cd06)

Eğer (izomorfik hariç) tensör ürünü belirtmektedir vektör uzayı tensör ürün , genel özelliği vektör uzayı bir izomorfizm kurar (not: Bir lineer olduğu alan ve çoklu doğrusal dönüşümlerin alan mekanların vektörü doğal olarak):



Bu eşlemenin sübjektivitesi varoluş ifadesi ile eş anlamlıdır (“her çok-doğrusal eşleme için vardır”, cf. ikinci ayna noktası), enjektivite ise benzersizlik ifadesine (“açıkça belirlenmiş bir”) eşdeğerdir. Verilen eşleme doğrusal bir eşleme (vektör uzaylarının homomorfizmi) olduğundan, vektör uzaylarının bir izomorfizmidir.
Eğer dikkate alınan tüm vektör uzayları sonlu boyutlu ise, bu durumda durum için iki vektör uzayı
kullanılabilir.

Birbirleriyle doğal olarak özdeşleşme, d. yani , karşılık gelen çok doğrusal formların öğeleri


1. ve 2. dereceden tensörlerin değişmezleri
Değişmezleri altında değişmeyen skalarlar olan tensör bir veya iki kademeli tensörünün koordinat dönüşümleri ortogonal. Birinci dereceden tensörler için, skaler çarpım tarafından indüklenen normun oluşumu bir değişmeze yol açar.
-
 ,
,
Burada ve aşağıda, Einstein'ın toplama kuralı tekrar kullanılmaktadır. Üç boyutlu Öklid uzayında ikinci dereceden tensörler için, genellikle altı indirgenemez değişmez (yani, diğer değişmezler tarafından ifade edilemeyen değişmezler) bulunabilir:

Simetrik 2. dereceden tensörler durumunda (örneğin, gerinim tensörü ) değişmezler ve çakışırlar. Ek olarak, diğer 3 değişmez de temsil edilebilir (böylece artık indirgenemez). Belirleyici aynı zamanda bir değişiklik göstermez; bu için, örneğin, temsil edilebilir indirgenemez değişmezler fazla matrisler , ve olduğu gibi







Antisymmetric tensörlerin için geçerlidir , , ve tekrar edilebilir bağladı. Böylece, üç boyutlu Öklid uzayında 2. seviyenin simetrik tensörlerinin üç indirgenemez değişmezi vardır ve 2. seviyenin antisimetrik tensörlerinin bir indirgenemez değişmezi vardır.





Bir vektör uzayının ve simetrinin tensör ürünleri
Bir vektör uzayının tensör ürünü kendisi ile oluşturulabilir. Vektör uzayı hakkında daha fazla bilgi olmadan , tensör çarpımının, saf çarpımlardaki faktörlerin değiş tokuşunu içeren bir otomorfizmi tanımlanabilir :




Bu eşlemenin karesi özdeşlik olduğu için özdeğerler için sadece değerlerin söz konusu olduğu sonucu çıkmaktadır .

- Bir o yerine getirmektir denir simetrik. Örnekler elementlerdir


-
 .
.
- Seviye 2'nin tüm simetrik tensörlerinin kümesi ile gösterilir.

- Bir o yerine getirmektir adlandırılır antisymmetric veya alternatif. Örnekler elementlerdir


-
 .
.
- Seviye 2'nin tüm antisimetrik tensörlerinin kümesi ile gösterilir.

Sayesinde tensör güçlerin herhangi bir seviyede oluşturulabilir. Buna uygun olarak, çiftler halinde daha fazla değişim tanımlanabilir. Ama bunlar artık birbirinden bağımsız değil. Bu şekilde, konumların her değişimi ve birinci konumla olan değişimlerin izleri geriye doğru izlenebilir:





Enjektif ve projektif tensör çarpımı
Birlikte gerdirilecek vektör uzayları bir topolojiye sahipse , onların tensör çarpımlarının da bir topolojiye sahip olması arzu edilir. Elbette böyle bir topolojiyi tanımlamanın birçok yolu vardır. Ancak, enjektif ve projektif tensör çarpımı bunun için doğal bir seçimdir.
tensör analizi
Başlangıçta, tensör hesabı burada sunulan modern cebirsel kavramda araştırılmamıştı, ancak diferansiyel geometri hakkındaki düşüncelerden ortaya çıktı. Özellikle Gregorio Ricci-Curbastro ve onu geliştiren öğrencisi Tullio Levi-Civita . Tensör hesabı bu nedenle Ricci hesabı olarak da adlandırılır. Albert Einstein , profesyonel dünyada iyi bilinmesini sağlayan görelilik teorisinde hesabı aldı . O zamanın tensörlerine şimdi tensör alanları deniyor ve bugün hala diferansiyel geometride önemli bir rol oynuyor. Tensörlerin aksine, tensör alanları, alttaki (genellikle eğri) uzayın her noktasına bir tensör atayan türevlenebilir eşlemelerdir.
Ayrıca bakınız
Edebiyat
-
Theodor Bröcker : Lineer Cebir ve Analitik Geometri. Birkhäuser , Basel 2004, ISBN 3-7643-2178-4 , bölüm. VII: Tensör hesabı.
-
Ralph Abraham , Jerrold E. Marsden , T. Ratiu: Manifoldlar, tensör analizi ve uygulamaları (= Uygulamalı matematik bilimleri. 75). 2. Baskı. Springer, New York NY ve ark. 1998, ISBN 0-387-96790-7 .
-
Theodore Frankel : Fiziğin Geometrisi. Giriş. Cambridge University Press, Cambridge ve diğerleri. 1997, ISBN 0-521-38334-X .
-
Horst Teichmann : Vektör ve tensör hesaplamalarının fiziksel uygulamaları (= BI üniversitesi cep kitapları . 39). 3. Baskı. Bibliographisches Institut , Mannheim ve ark. 1973, ISBN 3-411-00039-2 .
-
André Lichnerowicz : Tensör analizine giriş (= BI üniversitesi cep kitabı. 77). Bibliographisches Institut, Mannheim ve ark. 1966.
-
Horst Lippmann : Uygulamalı tensör hesabı. Springer 1993.
- Mikhail Itskov: Mühendisler için tensör cebiri ve tensör analizi. 3. Baskı. Springer, Heidelberg ve ark. 2013, ISBN 978-3-642-30878-9 .
-
Adalbert Duschk : Tensör kavramı ve fizik için anlamı. Kısım 1, 2, 3, Physikalische Blätter 1954, 1955, Kısım 1, Geometrik Temeller, Kısım 2, Tensalgebra, Kısım 3, Tensöranaliz.
-
Karin Reich : Tensör hesabının gelişimi. Mutlak diferansiyel hesaptan görelilik teorisine. Birkhäuser 1994 (tarih üzerine).
İnternet linkleri
- Georg Bernhardt: Tensörler, matrisler ve yalancı vektörler hakkında. PDF, Almanca, 340 kB.
- Joseph C. Kolecki: Fizik ve Mühendislik Öğrencileri için Tensörlere Giriş. Öğrenciler için tensör kalkülüsüne giriş, PDF, İngilizce, 328 kB, NASA yayını.
-
Özdeğer-Özvektör Glifleri: Bir Süreklilikte Sıfırıncı, İkinci, Dördüncü ve Yüksek Dereceli Tensörlerin Görselleştirilmesi. Vektörlerin görselleştirilmesi için web sitesi, İngilizce.
- Siegfried Petry: Tensör kalkülüsüne giriş.
Bireysel kanıt
-
↑ Bir temel tensör (veya basit tensör) sayısal bir değere (skaler) eşlenir.
-
↑ MMG Ricci, T. Levi-Civita: Méthodes de calccul différentiel absolu et leurs apps. İçinde: Matematiksel Yıllıklar. 54, 1901, ISSN 0025-5831 , s. 125-201, çevrimiçi.
-
^ John M. Lee: Pürüzsüz Manifoldlara Giriş (= Matematikte Lisansüstü Metinleri 218). Springer-Verlag, New York NY ve ark. 2003, ISBN 0-387-95448-1 , s. 172-179.
-
^ R. Abraham, Jerrold E. Marsden , T. Ratiu: Manifoldlar, tensör analizi ve uygulamaları (= Uygulamalı matematik bilimleri 75). 2. Baskı. Springer, New York NY ve ark. 1988, ISBN 0-387-96790-7 s. 338-339.
-
^ Kerstin Weinberg: Ders notları. Tensalgebra ve Analiz. (PDF; 235 kB) University of Siegen , 24 Ekim 2012, erişim tarihi 27 Kasım 2020 .
-
^ Heinz Schade, Klaus Neemann: Tensöranaliz . 2. gözden geçirilmiş baskı. de Gruyter, Berlin / New York 2006, ISBN 3-11-018943-7 , s. 277 ff .























































![{\ displaystyle {\ {matrix} L ^ {k} (E_ {1}, \ dotsc, E_ {k}; K) & {\ stackrel {\ sim} {\ longrightarrow}} & L (E_ {1} \ otimes \ dotsc \ otimes E_ {m}; E_ {m + 1} ^ {*} \ otimes \ dotsc \ otimes E_ {k} ^ {*}) \\\ lambda & \ longmapsto & \ sol [\ lambda _ { (1, \ dotsc, m)} \ kolon v_ {1} \ otimes \ dotsc \ otimes v_ {m} \ mapto \ lambda _ {(v_ {1}, \ dotsc, v_ {m})} \ in ( E_ {m + 1} \ bazen \ nokta \ bazen E_ {k}) ^ {*} \ sağ] {\ metin {,}} \\ && {\ metin {nerede}} \ sol [\ lambda _ {(v_) { 1}, \ dotsc, v_ {m})} \ iki nokta üst üste (v_ {m + 1} \ otimes \ dotsc \ otimes v_ {k}) \ mapto \ lambda (v_ {1}, \ dotsc, v_ {k} ) \ sağ] \\\ bitiş {matris}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5af0ca5982fcea7f59fe2aa8996dd0c3de44ce0)



























































































































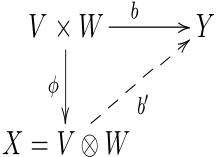




















































![{\ displaystyle \ psi: V_ {1} \ kez \ dotsb \ kez V_ {s} \ ila [??]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/597d0dd2574ad69e6b77499917be8e727960cd06)































