
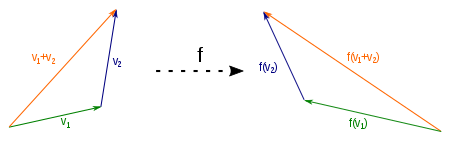
Doğrusal haritalama örneği olarak eksen yansıması
Bir doğrusal haritalama (aynı zamanda transformasyon doğrusal ya da vektör uzayı homomorfizmasının ) önemli bir tipi eşleme arasında iki vektör uzayı aynı fazla alanda doğrusal cebir . Doğrusal bir eşlemede, önce iki vektör ekleyip daha sonra bunların toplamını eşlemeniz veya önce vektörleri eşleştirmeniz ve ardından görüntülerin toplamını eklemeniz önemli değildir. Aynı şey , temel gövdeden bir skaler ile çarpma için de geçerlidir .
Y eksenindeki bir yansımanın gösterilen örneği bunu göstermektedir. Vektör vektörleri toplamıdır ve ve görüntü vektörüdür . Ama görüntüleri ve vektörleri eklerseniz ve .









Biri, doğrusal bir haritalamanın vektör toplama ve skaler çarpma kombinasyonlarıyla uyumlu olduğunu söylüyor . Doğrusal haritalama bu nedenle vektör uzayları arasında bir homomorfizmdir (yapıyı koruyan haritalama).
Olarak fonksiyonel analiz , sonsuz boyutlu vektör alanları dikkate taşıyan bir topoloji , bir genellikle söz doğrusal operatör yerine Lineer dönüşümlerin. Resmi bir bakış açısından, terimler eş anlamlıdır. Bununla birlikte, sonsuz boyutlu vektör uzayları söz konusu olduğunda, süreklilik sorunu önemliyken, süreklilik her zaman sonlu boyutlu gerçek vektör uzayları (her biri Öklid normuna sahip ) veya daha genel olarak sonlu boyutlu uzaylar arasındaki doğrusal eşlemelerde mevcuttur. Hausdorff topolojik vektör uzayları .
tanım
Olmak ve ortak bir temel gövde üzerinde vektör uzayları . Bir haritalama tüm eğer doğrusal haritalama denir ve aşağıdaki koşullar geçerlidir:






-
 homojendir:
homojendir:

-
 katkı maddesidir:
katkı maddesidir:

Yukarıdaki iki koşul da özetlenebilir:

Çünkü bu, homojenlik ve toplamsallık için koşullara girer . Diğer bir eşdeğer koşul, eşlemenin grafiğinin vektör uzaylarının toplamının bir alt uzayı olması gerekliliğidir ve .





Açıklama
Vektör uzayı yapısıyla uyumluysa bir eşleme doğrusaldır. Başka bir deyişle: doğrusal eşlemeler, tanım ve değer alanının temelindeki toplama ve skaler çarpım ile uyumludur. Ekleme ile uyumluluk, doğrusal eşlemenin toplamları aldığı anlamına gelir . Bir miktar varsa ile tanımlı olarak alan, daha sonra bu toplam geçerlidir ve bu nedenle çizimde uygun değer alanında kalır:





Bu ima önermeyi koyarak kısaltılabilir içinde . Talebi bu şekilde alırsınız . Skaler çarpımla uyumluluk benzer şekilde açıklanabilir. O, bu yerine getirilir aşağıdaki bağlantıdan skalar ile ve tanımı içinde aralıkta şu da o değer aralığında geçerlidir:








Öncülü sonuca ekledikten sonra kişi talep alır .



Skaler çarpım ile uyumluluğun görselleştirilmesi: Her ölçeklendirme doğrusal bir haritalama ile korunur ve uygulanır .


Örnekler
- İçin her doğrusal haritalama şekline sahiptir ile .



- Olması ve . Daha sonra doğrusal bir eşleme olan tanımlanmış her biri için bir matris yardımıyla matris çarpımı . Dan herhangi doğrusal haritalama için bu şekilde temsil edilebilir.








- Mı açık aralık arasında sürekli türevlenebilir fonksiyonların vektör alan ve sürekli fonksiyonların vektör alanı resmidir, yani , , her bir fonksiyon türevi, doğrusal atar. Aynısı diğer doğrusal diferansiyel operatörler için de geçerlidir .










Bu rakam toplamadır: Sadece vektörlerin eklenmesi ve ardından haritalanması veya sadece vektörlerin eşlenip ardından eklenip eklenmemesi önemli değildir .

Bu rakam homojen geçerli: Yalnızca sonra vektör ve haritalama ölçekli eğer önemli değil yoksa sadece eşler olup olmadığını ve daha sonra vektör ölçekler: .

Görüntü ve çekirdek
Öneme İki set doğrusal haritalar bakarak olan görüntü ve çekirdek bir lineer .

- Görüntü gösterim Aşağıdaki görüntü vektörleri kümesi , yani tüm grubu ile dışarı . Bu nedenle görüntülerin miktarı da belirtilir. Görüntü olduğu alt uzay arasında .







- Çekirdek haritalama vektörleri kümesi olan eşlenmiş üzerine sıfır vektör arasında göre. Bir alt uzayıdır . Eşleme , yalnızca ve ancak çekirdek yalnızca sıfır vektörünü içeriyorsa , enjekte edilir.






özellikleri
- Vektör uzayları arasındaki doğrusal bir harita ve sıfır vektörünün sıfır vektörünü şuradan oluşturur: çünkü






- Homomorfizmi teoremi tarif çekirdek ve bir doğrusal haritalama görüntü arasında bir ilişki : faktörü alanı olan izomorfik görüntü .



Sonlu boyutlu vektör uzayları arasında doğrusal eşlemeler
Baz

Enjeksiyon ve örten doğrusal eşlemelerin özelliklerinin özeti
Sonlu boyutlu vektör uzayları arasındaki doğrusal bir eşleme, bir temelin vektörlerinin görüntüleri tarafından benzersiz bir şekilde belirlenir. Vektörler oluşturuyorsa vektör alanının bir dayanak ve vardır içinde vektörler , daha sonra tam olarak bir doğrusal haritalama yoktur haritalar üzerine , üzerine , ..., üzerine . Herhangi bir vektör kapalıysa , temel vektörlerin doğrusal bir kombinasyonu olarak açıkça temsil edilebilir :














İşte koordinatları vektörü tabana göre . Onun görüntüsü verilir





Haritalama , ancak ve ancak temele ait görüntü vektörleri doğrusal olarak bağımsızsa , enjekte edicidir . Sadece ve ancak hedef bölgeyi kapsıyorsa kapsayıcıdır .




Bir vektörün bir tabanının her bir elemanına keyfi olarak atanırsa, bu nedenle yukarıdaki formülle doğrusal bir eşleme mümkündür, bu atama açıkça devam eder.





Görüntü vektörleri bir tabanına göre temsil edilirse , bu doğrusal eşlemenin matris gösterimine götürür.


Eşleme matrisi
Mı ve sonlu , ve bazlar arasında ve gelen , her bir doğrusal eşleme nerede bir yan - matris sunulmaktadır. Bu, aşağıdaki şekilde elde edilir: Her temel vektör için , görüntü vektörü , temel vektörlerin doğrusal bir kombinasyonu olarak temsil edilebilir :
















, , Matris girişleri şunlardır :





İnci kolon koordinatlarını içeren tabana göre .



Bu matrisin yardımıyla her vektörün
görüntü vektörü hesaplanabilir :



Saygı koordinatları için çok doğru



-
 .
.
Bu, matris çarpımı kullanılarak ifade edilebilir:

Matris , eşleme matrisi veya temsil matrisi olarak adlandırılır . Diğer yazımlar vardır ve .




![_ {B '} [f] _B](https://wikimedia.org/api/rest_v1/media/math/render/svg/062cd3a0f31d7327c7da18cc418a016a9c4a0279)
Boyutlu formül
Görüntü ve çekirdek, boyutlar kümesiyle ilişkilendirilir. Bu, boyutun görüntünün ve çekirdeğin boyutlarının toplamına eşit olduğunu belirtir :


Sonsuz boyutlu vektör uzayları arasında doğrusal eşlemeler
Özellikle fonksiyonel analizde , sonsuz boyutlu vektör uzayları arasındaki doğrusal eşlemeler dikkate alınır. Bu bağlamda, doğrusal eşleştirmeler genellikle doğrusal operatörler olarak adlandırılır. Dikkate alınan vektör uzayları, genellikle normalleştirilmiş bir tam vektör uzayının ek yapısına da sahiptir . Bu tür vektör uzaylarına Banach uzayları denir . Sonlu boyutlu durumun aksine, doğrusal operatörleri yalnızca bir temelde incelemek yeterli değildir. Göre Baier kategorisi teoremi , sonsuz boyutlu Banach alan bir baz, bir sahiptir sayılamaz sadece yani kullanılarak, yapısal olarak haklı olamaz elemanların sayısı ve böyle bir temelin varlığını aksiyomu bir seçim . Bu nedenle, ortonormal tabanlar veya daha genel olarak titreyen tabanlar gibi farklı bir temel terim kullanılır . Bu, Hilbert-Schmidt operatörleri gibi belirli operatörlerin "sonsuz büyük matrisler" kullanılarak gösterilebileceği ve böylece sonsuz doğrusal kombinasyonlara da izin verilmesi gerektiği anlamına gelir.
Özel doğrusal haritalar
- Monomorfizm
- Vektör uzayları arasındaki bir monomorfizm , enjekte edici olan doğrusal bir haritalamadır . Temsil matrisinin sütun vektörlerinin doğrusal olarak bağımsız olması durumunda durum budur.

- Epimorfizm
- Vektör uzayları arasındaki bir epimorfizm , örten olan doğrusal bir haritalamadır . Bu, ancak ve ancak temsil matrisinin sırası boyutuna eşitse geçerlidir .


- İzomorfizm
- Vektör uzayları arasındaki bir izomorfizm , bijektif olan doğrusal bir haritalamadır . Bu tam olarak ekran matrisinin düzenli olduğu durumdur. İki boşluk ve ardından izomorfik olarak adlandırılır.



- Endomorfizm
- Bir Endomorfizma vektör uzayı arasındaki boşluklar içinde doğrusal bir harita, ve eşittir: . Bu şeklin temsil matrisi bir kare matristir.



- Otomorfizm
- Bir otomorfizma vektör uzayı arasındaki boşluklar olan bir örten doğrusal eşleme ve vardır buna eşittir. Yani hem izomorfizm hem de endomorfizmdir. Bu şeklin gösterim matrisi düzenli bir matristir.


Doğrusal şekiller vektör uzayı

Vektör uzayının oluşumu L (V, W)
Set bir gelen doğrusal dönüşümlerinin -vector alanına bir içine -vector alanı üzerinde bir vektör alanıdır bir alt uzay: daha doğrusu, tüm eşleme -vector alanı için . Bu, iki doğrusal haritanın toplamının ve bileşen olarak tanımlanan












yine doğrusal bir eşlemedir ve ürün

skaler ile doğrusal bir eşleme de yine doğrusal bir eşlemedir .

Eğer boyut ve boyut ve verilmiştir temel ve temel , daha sonra eşleme olduğunu









Bir izomorfizm olarak matris alanı . Dolayısıyla vektör uzayı boyuta sahiptir .



Bir vektör alanı, yani, özel bir durum doğrusal öz eşleme grubu gördüğü takdirde daha sonra bu, sadece bir vektör alanı, aynı zamanda meydana birleştirici cebir çarpma gibi dönüşümlerin birleştirme ile kısaca, şu şekilde de ifade


genelleme
Doğrusal bir haritalama, afin haritalamanın özel bir durumudur .
Vektör uzayları arasındaki doğrusal eşleme tanımında cisim bir halka ile değiştirilirse , bir modül homomorfizmi elde edilir .
Notlar ve bireysel referanslar
-
↑ Bu doğrusal eşleme kümesi bazen olarak da yazılır.

Edebiyat
-
Albrecht Beutelspacher : Doğrusal Cebir. Vektörler, haritalar ve matrisler bilimine giriş. 6., gözden geçirilmiş ve tamamlanmış baskı. Vieweg Braunschweig ve diğerleri 2003, ISBN 3-528-56508-X , sayfa 124-143.
- Günter Gramlich: Doğrusal Cebir. Mühendisler için bir giriş. Fachbuchverlag Leipzig, Carl-Hanser-Verlag, Münih 2003, ISBN 3-446-22122-0 .
- Detlef Wille: Doğrusal Cebirin Tekrarı. Cilt 1. 4. baskı, yeniden yazdırın. Binomi, Springe 2003, ISBN 3-923923-40-6 .
İnternet linkleri


















































































































![_ {B '} [f] _B](https://wikimedia.org/api/rest_v1/media/math/render/svg/062cd3a0f31d7327c7da18cc418a016a9c4a0279)















