Tek adımlı süreç

Yöntem ile bir ilk değer sorun çözeltisi (mavi) yaklaşık Tek aşamalı belirleme noktaları , vb birbiri ardına belirli bir başlangıç noktasından${\ görüntü stili A_ {0}}$${\ görüntü stili A_ {1}}$${\ görüntü stili A_ {2}}$

Olarak sayısal matematik, tek-aşamalı bir yöntem olarak, olan ek çok-aşamalı yöntem, büyük bir grup hesaplama yöntemleri çözmek için başlangıç değer problemleri . Bir başlangıç ​​koşulu ile birlikte ortak bir diferansiyel denklemin verildiği bu görev, tüm doğa ve mühendislik bilimlerinde merkezi bir rol oynamaktadır ve örneğin ekonomi ve sosyal bilimlerde giderek daha önemli hale gelmektedir. Başlangıç ​​değer problemleri, dinamik süreçleri analiz etmek, simüle etmek veya tahmin etmek için kullanılır.

Tek adımlı yöntemin isim veren temel fikri, verilen başlangıç ​​noktasından başlayarak, aranan çözüm boyunca adım adım yaklaşım noktalarını hesaplamalarıdır. Bunu yaparken, hesaplamada daha geride kalan noktaları da içeren çok adımlı yöntemin aksine, yalnızca bir sonraki adım için en son belirlenen yaklaşımı kullanırlar. Tek adımlı yöntemler kabaca iki gruba ayrılabilir: yeni yaklaşımı doğrudan eskisinden hesaplayan açık yöntemler ve bir denklemin çözülmesi gereken kapalı yöntemler. İkincisi, katı başlangıç ​​değeri problemleri olarak adlandırılan problemler için de uygundur .

En basit ve en eski tek adımlı yöntem, açık Euler yöntemi , Leonhard Euler tarafından 1768'de yayınlandı . 1883'te bir grup çok adımlı süreç sunulduktan sonra, 1900 civarında Carl Runge , Karl Heun ve Wilhelm Kutta , Euler'in sürecinde önemli iyileştirmeler geliştirdiler . Bunlardan , tek adımlı süreçlerin en önemli sınıfını oluşturan büyük Runge-Kutta süreçleri grubu ortaya çıktı . 20. yüzyılın diğer gelişmeleri, örneğin, ekstrapolasyon fikridir , ancak her şeyden önce adım boyutu kontrolü, yani bir yöntemin bireysel adımları için uygun uzunlukların seçimi için hususlar. Bu kavramlar, modern uygulamalarda ortaya çıktıkları için, bilgisayar programlarını kullanarak verimli ve gerekli doğrulukla zor başlangıç ​​değer problemlerini çözmenin temelini oluşturur.

Giriş

Adi diferansiyel denklemler

17. yüzyılın son üçte birinde İngiliz fizikçi ve matematikçi Isaac Newton ve ondan bağımsız olarak Alman bilge Gottfried Wilhelm Leibniz tarafından diferansiyel ve integral hesabın geliştirilmesi , erken modern dönemde bilimin matematikleştirilmesi için önemli bir itici güçtü . Bu yöntemler, matematiksel analiz dalının başlangıç ​​noktasını oluşturmuştur ve tüm doğa ve mühendislik bilimlerinde merkezi öneme sahiptir. Leibniz, diferansiyel hesap için verilen eğrilere teğetleri belirleme geometrik problemi tarafından yönlendirilirken, Newton belirli bir zamanda fiziksel bir nicelikteki değişikliklerin nasıl belirlenebileceği sorusundan yola çıktı.

Örneğin, bir cisim hareket ettiğinde, ortalama hızı basitçe kat edilen mesafenin aldığı zamana bölünmesidir. Bununla birlikte, vücudun belirli bir zaman noktasındaki mevcut hızını matematiksel olarak formüle etmek için bir sınır geçişi gereklidir: Kısa uzunluk periyotları , kat edilen mesafeler ve ilgili ortalama hızlar dikkate alınır . Eğer kişi sağlayan zaman aralığı sıfıra yakınsar ve ortalama halinde hızları da yaklaşım , sabit bir değer , bu değer (anlık) hızı olarak adlandırılır zaman içinde belirli bir noktada . Açıklar zamanda vücudun pozisyonunu sonra bir yazar ve isimleri türetme arasında . ${\ görüntü stili v (t)}$${\ görüntü stili t}$${\ görüntü stili \ Delta t}$${\ görüntü stili \ Delta x}$${\ görüntü stili {\ tfrac {\ Delta x} {\ Delta t}}}$${\ görüntü stili \ Delta t}$${\ görüntü stili v (t)}$${\ görüntü stili t}$${\ görüntü stili x (t)}$${\ görüntü stili t}$${\ görüntü stili v (t) = x '(t)}$${\ görüntü stili v}$${\ görüntü stili x}$

Diferansiyel denklem modelleri yönündeki belirleyici adım şimdi tam tersi sorudur: Hareket eden cisim örneğinde , hız her zaman bilinir ve konumu bundan belirlenecektir. Bu sorunu net bir şekilde çözebilmek için , vücudun ilk pozisyonunun da belirli bir zamanda bilinmesi gerektiği çok açıktır. Bu bir fonksiyonudur ait o ilk şartı arıyor verilen değerlerle ve yerine getirdi. ${\ görüntü stili t}$${\ görüntü stili v (t)}$${\ görüntü stili x (t)}$${\ görüntü stili t_ {0}}$${\ görüntü stili x (t)}$${\ görüntü stili x '(t) = v (t)}$${\ görüntü stili x (t_ {0}) = x_ {0}}$${\ görüntü stili t_ {0}}$${\ görüntü stili x_ {0}}$

Bir cismin hızından konumunu belirleme örneğinde, aranan fonksiyonun türevi açıkça verilmiştir. Bununla birlikte genellikle, gerekli bir miktar için diferansiyel denklemlerin önemli genel durum vardır : Doğanın yasa veya model varsayımlarına dayanarak, işlevsel bir ilişki olduğunu türetilmesi nasıl gösterir bilinen fonksiyonu belirlenecek hesaplanabilir dan ve (bilinmeyen) değerinden . Ek olarak, örneğin zaman içinde sabit bir noktada gerekli değişkenin ölçümünden elde edilebilecek bir başlangıç ​​koşulu yine olmalıdır . Özetle, aşağıdaki genel problem tipine sahibiz: Denklemleri içeren fonksiyonu bulun${\ görüntü stili x}$${\ görüntü stili y}$${\ görüntü stili y '(t)}$${\ görüntü stili t}$${\ görüntü stili y (t)}$${\ görüntü stili y}$

${\ displaystyle y '(t) = f (t, y (t)), \ dörtlü y (t_ {0}) = y_ {0}}$

verilen bir fonksiyon nerede . ${\ görüntü stili f}$

Lorenz çekicisinin diferansiyel denkleminin sunulan çözümü, üç boyutlu uzayda çok karmaşık bir eğridir.

Basit bir örnek, bir boyutudur katlanarak büyür . Güncel değişim, diğer bir deyişle türevi olan bu araçlar orantılı için tek başına. Dolayısıyla bir büyüme oranı ve örneğin bir başlangıç ​​koşulu ile uygulanır . Bu durumda aradığınız çözüm , elementer diferansiyel hesap ile zaten bulunabilir ve üstel fonksiyon yardımıyla belirtilebilir: Uygulanır . ${\ görüntü stili y}$${\ görüntü stili y '(t)}$ ${\ görüntü stili y (t)}$${\ displaystyle y '(t) = \ lambda y (t)}$${\ görüntü stili \ lambda}$${\ görüntü stili y (0) = y_ {0}}$${\ görüntü stili y}$${\ displaystyle y (t) = y_ {0} e ^ {\ lambda t}}$

Aranan işlevi olabilir diferansiyel denklemdeki vektör değerli olduğunu, her biri için orada olabilir bir vektör ile bileşenler. Daha sonra bir boyutlu diferansiyel denklem sisteminden bahsediliyor. Bir hareket parçası durumunda, içindeki konumu boyutlu Öklid alan ve onun hızı daha sonra bir zamanda . Bu nedenle diferansiyel denklem, zaman ve uzaydaki her noktada yön ve büyüklük ile aranan yörüngenin hızını belirtir. Yolun kendisi bundan hesaplanmalıdır. ${\ görüntü stili y}$${\ görüntü stili t}$${\ displaystyle y (t) = (y_ {1} (t), \ dotsc, y_ {d} (t))}$${\ görüntü stili d}$${\ görüntü stili d}$${\ görüntü stili y (t)}$${\ görüntü stili d}$${\ görüntü stili y '(t)}$${\ görüntü stili t}$

Tek adımlı sürecin temel fikri

Yukarıda örnek olarak ele alınan üstel büyümenin basit diferansiyel denklemi ile çözüm fonksiyonu doğrudan belirtilebilir. Genel olarak, bu daha karmaşık problemlerde artık mümkün değildir. Belirli ek koşullar altında , ilk değer probleminin benzersiz olarak belirlenmiş bir çözümünün mevcut olduğu fonksiyon için gösterilebilir; Bununla birlikte, bu durumda artık olabilir açıkça kullanılarak hesaplanmıştır analiz yöntemleri (örneğin, değişkenlerin ayrılması , bir üstel bir yaklaşım veya sabitlerin değişimi ). Bu durumda, aranan çözüme yaklaşmak için sayısal yöntemler kullanılabilir. ${\ görüntü stili f}$

Adi diferansiyel denklemlerin başlangıç ​​değer problemlerinin sayısal çözümü için yöntemler kabaca iki büyük gruba ayrılabilir: tek adımlı ve çok adımlı yöntem. Her iki grubun ortak noktası, noktalarda istenen fonksiyon değerleri için kademeli olarak yaklaşımları hesaplamalarıdır . Tek adımlı yöntemin tanımlayıcı özelliği, aşağıdaki yaklaşımı belirlemek için yalnızca "geçerli" yaklaşımın kullanılmasıdır. Bunun aksine, çok adımlı yöntemlerde önceden hesaplanmış yaklaşımlar da dahil edilir; üç aşamalı bir yöntemi , bu nedenle, örneğin, olur aynı zamanda kullanımı ve yeni bir yaklaşım belirlenmesi . ${\ görüntü stili y_ {0}, y_ {1}, y_ {2}, \ noktalı}$${\ görüntü stili y (t_ {0}), y (t_ {1}), y (t_ {2}), \ noktasal}$${\ displaystyle t_ {0} <t_ {1} <t_ {2} <\ ldots}$${\ görüntü stili y_ {j + 1}}$${\ görüntü stili y_ {j}}$${\ görüntü stili y_ {j}}$${\ görüntü stili y_ {j-1}}$${\ görüntü stili y_ {j-2}}$${\ görüntü stili y_ {j + 1}}$

Açık Euler yönteminin iki adımı

En basit ve en temel tek adımlı yöntem, İsviçreli matematikçi ve fizikçi Leonhard Euler'in 1768'de Institutiones Calculi Integralis adlı ders kitabında sunduğu açık Euler yöntemidir . Bu yöntemin fikri, bir parça-bazlı doğrusal fonksiyonu tarafından aranan solüsyona yaklaşmak için düz çizgi eğimi olan belirli bir noktadan, her aşamada noktasına . Daha doğrusu: Problem zaten aranan fonksiyon için bir değer veriyor, yani . Ancak bu noktada türetme de bilinmektedir, çünkü geçerlidir . Çözüm fonksiyonunun grafiğine teğet böylece belirlenebilir ve bir yaklaşım olarak kullanılabilir. Bu noktada bir adım boyutu var${\ görüntü stili t_ {j}}$${\ görüntü stili t_ {j + 1}}$${\ görüntü stili f (t_ {j}, y_ {j})}$${\ görüntü stili y (t_ {0}) = y_ {0}}$${\ displaystyle y '(t_ {0}) = f (t_ {0}, y_ {0})}$${\ görüntü stili t_ {1}> t_ {0}}$${\ displaystyle h_ {0}: = t_ {1} -t_ {0}}$

${\ displaystyle y (t_ {1}) \ yaklaşık y_ {0} + h_ {0} f (t_ {0}, y_ {0}) =: y_ {1}}$.

Bu prosedür artık aşağıdaki adımlarda devam ettirilebilir. Genel olarak, bu, açık Euler yöntemi için hesaplama kuralıyla sonuçlanır.

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} f (t_ {j}, y_ {j}), \ dörtlü j = 0,1,2, \ noktasal}$

adım boyutları ile .${\ displaystyle h_ {j} = t_ {j + 1} -t_ {j}}$

Açık Euler yöntemi, eğimin, noktalar arasındaki çözümün davranışına yaklaşan ve daha kesin olarak eğimlerle değiştirildiği çok sayıda genelleme için başlangıç ​​noktasıdır . Eğim olarak kullanılan örtük Euler yöntemi, tek adımlı yöntemler için ek bir fikir sağlar . İlk bakışta bu seçim bilinmediği için uygun görünmüyor . Denklem şimdi bir prosedür adımı olarak elde edilir ${\ görüntü stili f (t_ {j}, y_ {j})}$${\ görüntü stili t_ {j}}$${\ görüntü stili t_ {j + 1}}$${\ görüntü stili f (t_ {j + 1}, y_ {j + 1})}$${\ görüntü stili y_ {j + 1}}$

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} f (t_ {j + 1}, y_ {j + 1})}$

buradan (gerekirse sayısal bir yöntemle) hesaplanabilir. Örneğin, açık ve kapalı Euler yönteminin eğimlerinin aritmetik ortalaması eğim olarak seçilirse, örtük yamuk yöntemi elde edilir . Bundan açık bir yöntem elde edilebilir, örneğin, Heun yöntemi olarak adlandırılan açık Euler yöntemini yaklaştırarak denklemin sağ tarafındaki bilinmeyene yaklaşırsak . Tüm bu prosedürler ve diğer tüm genellemeler, ortak olarak tek adımlı prosedürün temel fikrine sahiptir: adım ${\ görüntü stili y_ {j + 1}}$${\ görüntü stili y_ {j + 1}}$

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} \ Phi}$

bir eğim ile bağlı olabilir , ve (kapalı metodlar durumunda) ve ilgili. ${\ görüntü stili \ Phi}$${\ görüntü stili t_ {j}}$${\ görüntü stili y_ {j}}$${\ görüntü stili h_ {j}}$${\ görüntü stili y_ {j + 1}}$

tanım

Bu makalenin giriş bölümündeki düşüncelerle, tek adımlı prosedür kavramı şu şekilde tanımlanabilir: Başlangıç ​​değer problemine çözüm arıyoruz.${\ görüntü stili y}$

${\ görüntü stili y '(t) = f (t, y (t))}$, .${\ displaystyle \ dörtlü y (t_ {0}) = y_ {0}}$

Çözümün olduğu varsayılıyor

${\ displaystyle y \ iki nokta üst üste I \ to \ mathbb {R} ^ {d}}$

belirli bir aralıkta bulunur ve benzersiz bir şekilde belirlenir. vardır ${\ görüntü stili I = [t_ {0}, T]}$

${\ displaystyle t_ {0} <t_ {1} <t_ {2} <\ ldots <t_ {n} = T}$

Aralıktaki ara noktalar ve ilişkili adım boyutları, o zaman bu, şu anlama gelir: ${\ görüntü stili I}$${\ displaystyle h_ {j} = t_ {j + 1} -t_ {j}}$

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} \ Phi (t_ {j}, y_ {j}, y_ {j + 1}, h_ {j})}$, ${\ displaystyle \ dörtlü j = 0, \ dotsc, n-1}$

verilen prosedürler , prosedür fonksiyonu ile tek adımlı prosedür . O takdirde vermez bağlıdır, o zaman bir denir açık tek adımlı prosedür . Aksi takdirde, her adımda bir denklemin çözülmesi gerekir ve prosedüre örtük denir.${\ görüntü stili \ Phi}$${\ görüntü stili \ Phi}$${\ görüntü stili y_ {j + 1}}$${\ görüntü stili j}$${\ görüntü stili y_ {j + 1}}$

Tutarlılık ve Yakınsama

yakınsama sırası

Üç tek adımlı yöntem için farklı adım boyutlarında global hata . Bir de çift logaritmik arsa , ilişki yamaçları yakınsama siparişler 1, 2 ve 4 tekabül yaklaşık lineer görünür.${\ görüntü stili h}$

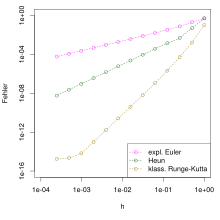
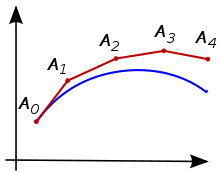
Pratik tek adımlı bir yöntem için , kesin çözümün değerleri için hesaplanan iyi yaklaşımlar noktasında olmalıdır . Miktarlar genellikle boyutlu vektörler olduğundan, bu yaklaşımın kalitesi , noktasındaki hata gibi bir vektör normu ile ölçülür . Adım boyutlarının sıfıra yakınsamasına izin verilirse , bu hataların tümü için hızla sıfıra yakınsaması arzu edilir . Ayrıca sabit olmayan aşama boyutunda durumunda karşılamak için, bir tanımlar, bu daha kesin aşamasının en kullanılmış ve tüm noktalarda maksimum hata davranışı dikkate boyutları olarak yetkilerine karşılaştırıldığında . Verilen ilk değer problemini çözmek için tek adımlı prosedürün, eğer tahmin yapılırsa yakınsama sırasına sahip olduğu söylenir.${\ görüntü stili y_ {j}}$${\ görüntü stili y (t_ {j})}$${\ görüntü stili y}$${\ görüntü stili t_ {j}}$${\ görüntü stili d}$${\ görüntü stili \ | y_ {j} -y (t_ {j}) \ |}$${\ görüntü stili t_ {j}}$${\ görüntü stili j}$${\ görüntü stili h}$${\ görüntü stili t_ {j}}$${\ görüntü stili h}$ ${\ displaystyle p \ geq 1}$

${\ displaystyle \ max _ {j = 0, \ dotsc, n} \ | y_ {j} -y (t_ {j}) \ | \ leq Ch ^ {p}}$

'den bağımsız bir sabite sahip yeterince küçük olan her şey için geçerlidir.${\ görüntü stili h}$${\ görüntü stili h}$${\ görüntü stili C> 0}$

Yakınsama sırası, farklı tek adımlı prosedürleri karşılaştırmak için en önemli parametredir. Daha yüksek yakınsama derecesine sahip bir yöntem, genellikle belirli bir adım boyutu için daha küçük bir toplam hata verir veya tersine, belirli bir doğruluğu elde etmek için daha az adım gerekir. İle bir yöntem söz konusu olduğunda, adım boyutu yarıya indirilirse, hatanın yalnızca kabaca yarıya indirilmesi beklenir. Yakınsama mertebesine sahip bir yöntem söz konusu olduğunda, hatanın yaklaşık olarak faktör kadar azaldığı varsayılabilir . ${\ görüntü stili p}$${\ görüntü stili p = 1}$${\ görüntü stili p = 4}$${\ displaystyle {\ bigl (} {\ tfrac {1} {2}} {\ bigr)} ^ {4} = {\ tfrac {1} {16}}}$

Küresel ve yerel hata

Yakınsama düzeninin tanımında ele alınan hatalar , başlangıçta karmaşık görünecek şekilde iki ayrı bileşenden oluşur: Elbette, bir yandan prosedürün tek bir adımda yaptığı hataya bağlıdırlar, çünkü aranan fonksiyonun bilinmeyen eğimi, Prosedürel fonksiyon yaklaşıkları ile değiştirilir. Öte yandan, bir adımın başlangıç ​​noktasının genellikle tam başlangıç ​​noktasıyla zaten çakışmadığı da dikkate alınmalıdır ; bu adımdan sonraki hata , önceki adımlarda yapılmış olan tüm hatalara da bağlıdır . Yalnızca prosedürel işlevin seçiminde farklılık gösteren tek adımlı prosedürün tek tip tanımı nedeniyle , (belirli teknik koşullar altında ) tek bir adımda doğrudan hata sıralamasından yakınsama sırasının çıkarılabileceği kanıtlanabilir , sözde tutarlılık sırası. ${\ görüntü stili \ | y_ {j} -y (t_ {j}) \ |}$${\ görüntü stili (t_ {j}, y_ {j})}$${\ görüntü stili (t_ {j}, y (t_ {j}))}$${\ görüntü stili \ Phi}$${\ görüntü stili \ Phi}$

Kavramı tutarlılık Modern sayısal matematik genel ve merkezi bir kavramdır. Bir prosedürün yakınsaması sırasında sayısal yaklaşımların kesin çözüme ne kadar iyi uyduğunu incelerken, tutarlılık söz konusu olduğunda, basitçe söylemek gerekirse, “zıt” soru sorulur: Kesin çözüm, prosedürel belirtimi ne kadar iyi karşılıyor? Bu genel teoride, bir yöntemin ancak ve ancak tutarlı ve kararlı olması durumunda yakınsak olduğunu kabul eder . Gösterimi basitleştirmek için, aşağıdaki dikkate alındığında açık bir tek adımlı prosedürün olduğu varsayılmalıdır.

${\ displaystyle y_ {j + 1} = y_ {j} + h \ Phi (t_ {j}, y_ {j}, h)}$

sabit bir adım boyutu ile . Gerçek çözüm , yerel kırpma hatasını ( yerel prosedür hatası olarak da adlandırılır ) şu şekilde tanımlar:${\ görüntü stili h}$${\ displaystyle t \ mapto y (t)}$${\ görüntü stili \ eta}$

${\ displaystyle \ eta (t, h) = y (t) + h \ Phi (t, y (t), h) -y (t + h)}$.

Böylece, kesin çözümün bilindiği varsayılır, bu noktada bir işlem adımı başlatılır ve o noktada kesin çözümle olan fark oluşturulur . Bu tanımlar: Tek adımlı bir prosedür, tahminin tutarlılık sırasına sahiptir.${\ görüntü stili (t, y (t))}$${\ görüntü stili t + h}$ ${\ displaystyle p \ geq 1}$

${\ displaystyle \ | \ eta (t, h) \ | \ leq Ch ^ {p + 1}}$

bağımsız bir sabit ile yeterince küçük olan her şey için geçerlidir. ${\ görüntü stili h}$${\ görüntü stili h}$${\ görüntü stili C> 0}$

Tutarlılık sırası ve yakınsama sırası tanımları arasındaki göze çarpan fark, yerine güçtür . Bu, yerel hatadan küresel hataya geçiş sırasında adım boyutunun gücünün “kaybolacağı” şeklinde açık bir şekilde yorumlanabilir. Tek adımlı prosedür teorisinin merkezinde yer alan aşağıdaki teorem geçerlidir:${\ displaystyle h ^ {p + 1}}$${\ displaystyle h ^ {p}}$

İşlem fonksiyonu Lipschitz sürekli ise ve ilgili tek adımlı işlem tutarlılık sırasına sahipse, yakınsama sırasına da sahiptir .${\ görüntü stili \ Phi}$ ${\ görüntü stili p}$${\ görüntü stili p}$

Kararlılık için ek bir gereklilik olarak proses fonksiyonunun Lipschitz sürekliliği , diferansiyel denklemdeki fonksiyonun kendisi Lipschitz sürekli ise genellikle her zaman yerine getirilir . Başlangıç ​​değer probleminin kesin çözülebilirliğini garanti altına almak için çoğu uygulama için bu gereklilik zaten kabul edilmelidir. Teoreme göre, tek adımlı bir prosedürün tutarlılık sırasını belirlemek yeterlidir. Prensipte bu , ' nin kuvvetlerine bir Taylor açılımı ile başarılabilir . Uygulamada, daha yüksek dereceler için elde edilen formüller çok karmaşık ve kafa karıştırıcı hale gelir, bu nedenle ek kavramlar ve gösterimler gerekir.${\ görüntü stili f}$${\ displaystyle \ eta (t, h)}$${\ görüntü stili h}$

Sertlik ve A-kararlılığı

Bir yöntemin yakınsama sırası, adım boyutu sıfıra yakınsadığında yaklaşımların davranışını tanımlayan asimptotik bir ifadedir. Ancak, yöntemin belirli bir sabit adım boyutu için gerçekten kullanılabilir bir yaklaşıklık hesaplayıp hesaplamadığı hakkında hiçbir şey söylemez. Charles Francis Curtiss ve Joseph O. Hirschfelder ilk olarak 1952'de bunun belirli türdeki başlangıç ​​değer problemlerinde büyük bir problem olabileceğini açıkladılar ve kimyasal reaksiyon kinetiğinin bazı diferansiyel denklem sistemlerinin çözümlerinin açık kullanılarak hesaplanamayacağını gözlemlediler. sayısal yöntemler ve onlara bu tür başlangıç ​​değer problemlerini "sert" olarak adlandırdılar. Belirli bir problemin ne kadar katı olduğunu belirlemek için çok sayıda matematiksel kriter vardır. Açıkça, katı başlangıç ​​değeri problemleri, çoğunlukla, bazı bileşenlerin çok hızlı sabitlendiği, diğer bileşenlerin ise yalnızca yavaş değiştiği diferansiyel denklem sistemleridir. Bu tür davranışlar tipik olarak kimyasal reaksiyonları modellerken ortaya çıkar. Pratik uygulama için rijitliğin en kullanışlı tanımı şudur: Açık bir tek adımlı yöntemle kullanılabilir bir çözüm elde etmek için adım boyutunun “çok küçük” seçilmesi gerekiyorsa, bir başlangıç ​​değer problemi katıdır. Bu tür sorunlar ancak örtük yöntemlerle çözülebilir.

Üstel olarak düşen bir çözümü (mavi) hesaplamak için, adım boyutu çok büyükse açık Euler yöntemi (kırmızı) tamamen işe yaramaz; örtük Euler yöntemi (yeşil), herhangi bir adım boyutu için çözümü niteliksel olarak doğru bir şekilde belirler.

Bu etki, bireysel yöntemlerin üstel bozulma ile nasıl başa çıktığını inceleyerek daha kesin olarak gösterilebilir . Bunu yapmak için İsveçli matematikçi Germund Dahlquist'e göre test denklemini düşünün .

${\ displaystyle y '(t) = \ lambda y (t), \ dörtlü y (0) = 1}$

ile katlanarak azalan çözeltisi . Karşıdaki grafik - açık ve örtük Euler yönteminin bir örneği olarak - bu iki yöntem grubunun bu görünüşte basit başlangıç ​​değer problemindeki tipik davranışını gösterir: Açık bir yöntemde çok büyük bir adım boyutu kullanılırsa, o zaman güçlü bir şekilde salınım yapar. Hesaplamayı oluşturun ve kesin çözümden gittikçe uzaklaşan değerler sonucu. Öte yandan, örtük yöntemler, tipik olarak, herhangi bir adım boyutu için çözümü niteliksel olarak doğru bir şekilde hesaplar, yani katlanarak azalan yaklaşık değerler dizisi olarak.${\ görüntü stili \ lambda <0}$${\ displaystyle y (t) = e ^ {\ lambda t}}$

Yukarıdaki test denklemi ayrıca karmaşık değerler için biraz daha genel olarak kabul edilir . Bu durumda, çözeltiler titreşimler olan genlik kalıntıları eğer sınırlı uygulanabilir, yani gerçek bileşeni arasında ya da daha düşük 0 eşittir. Bu, katı başlangıç ​​değeri problemleri için kullanılacak olan tek adımlı yöntemlerin arzu edilen bir özelliğinin formüle edilmesini sağlar: A-kararlılığı olarak adlandırılan. Bir yöntem, herhangi bir adım boyutu için test denklemine uygulanırsa ve (gerçek çözüm gibi) kısıtlı kalan bir yaklaşım dizisi ile tümü için hesaplanırsa , A-kararlı olarak adlandırılır . Örtülü Euler yöntemi ve örtük yamuk yöntemi, A-kararlı tek adımlı yöntemlerin en basit örnekleridir. Öte yandan, açık bir prosedürün asla A-kararlı olamayacağı gösterilebilir.${\ görüntü stili \ lambda}$${\ displaystyle \ operatör adı {Re} (\ lambda) \ leq 0}$${\ görüntü stili \ lambda}$${\ görüntü stili h> 0}$${\ görüntü stili \ lambda}$${\ displaystyle \ operatör adı {Re} (\ lambda) \ leq 0}$${\ görüntü stili y_ {0}, y_ {1}, y_ {2}, \ noktalı}$

Özel prosedürler ve prosedür sınıfları

Karşılaştırmada bazı tek adımlı prosedürler

1. ve 2. sıradaki basit prosedürler

Fransız matematikçi olarak Augustin Louis Cauchy 1820 civarında kanıtladı yamaçları ise Euler yöntemi yakınsaması 1. sırasını sahip açık Euler yöntemiyle ve örtük Euler yöntemiyle bir adımın iki uç noktalarda bulunmaktadır gibi olabilir tüm aralık boyunca daha iyi bir yaklaşım elde etmek için ortalama umut. Aslında, bu şekilde elde edilen örtük yamuk yönteminin kanıtlanabilir.${\ görüntü stili f (t_ {j}, y_ {j})}$${\ görüntü stili f (t_ {j + 1}, y_ {j + 1})}$

${\ displaystyle y_ {j + 1} = y_ {j} + {\ frac {h} {2}} {\ Büyük (} f (t_ {j}, y_ {j}) + f (t_ {j + 1) }, y_ {j + 1}) {\ Büyük)}}$

yakınsama sırası 2'dir. Bu yöntem çok iyi kararlılık özelliklerine sahiptir, ancak örtüktür, bu nedenle her adımda bir denklemin çözülmesi gerekir. Bu nicelik, açık Euler yöntemi kullanılarak denklemin sağ tarafında yaklaşık olarak hesaplanırsa, Heun'un kesin yöntemi ortaya çıkar.${\ görüntü stili y_ {j + 1}}$

${\ displaystyle y_ {j + 1} = y_ {j} + {\ frac {h} {2}} {\ Büyük (} f (t_ {j}, y_ {j}) + f {\ büyük (} t_) {j + 1}, y_ {j} + hf (t_ {j}, y_ {j}) {\ büyük)} {\ Büyük)}}$,

bu da yakınsama sırasına sahiptir 2. 2. dereceden başka bir basit açık yöntem, geliştirilmiş Euler yöntemi , aşağıdakiler dikkate alınarak elde edilebilir: İşlem adımındaki bir "ortalama" eğim, adımın ortasındaki, yani noktasındaki çözümün eğimi olacaktır . Bununla birlikte, çözüm bilinmediğinden, adım boyutunun yarısı olan açık bir Euler adımı ile yaklaşık olarak hesaplanır. Usul kuralı sonuçları ${\ görüntü stili y}$${\ displaystyle t_ {j} + {\ tfrac {h} {2}}}$

${\ displaystyle y_ {j + 1} = y_ {j} + hf {\ büyük (} t_ {j} + {\ tfrac {h} {2}}, y_ {j} + {\ tfrac {h} {2 }} f (t_ {j}, y_ {j}) {\ büyük)}}$.

Bu tek adımlı 2. derece yöntemlerin tümü, 1895'te Alman matematikçi Carl Runge tarafından Euler yönteminde iyileştirmeler olarak yayınlandı .

Runge-Kutta yöntemi

Klasik dördüncü dereceden Runge-Kutta yöntemi, her adımda dört yardımcı eğimin (kırmızı) ortalamasını alır

Basit tek adımlı yöntemler için yukarıda bahsedilen fikirler, eğer daha fazla genelleştirilirlerse, Runge-Kutta yöntemlerinin önemli sınıfına götürür. Örneğin, Heun'un yöntemi şu şekilde daha açık bir şekilde sunulabilir: Önce yardımcı bir eğim hesaplanır, yani açık Euler yönteminin eğimi. Bu, burada başka bir yardımcı eğimi belirler . Gerçekte kullanılan işlem gradyanı, daha sonra Heun yönteminde yardımcı gradyanların ağırlıklı ortalaması olarak sonuçlanır . Bu prosedür, ikiden fazla yardımcı şev için genelleştirilebilir. Bir adımlı Runge-Kutta yöntemi önce yardımcı gradyanları uygun noktalarda değerlendirerek ve ardından ağırlıklı ortalama olarak hesaplar . Açık bir Runge-Kutta yöntemi durumunda, yardımcı eğimler birbiri ardına doğrudan hesaplanır; örtük bir yöntem durumunda, bir denklem sisteminin çözümleri olarak sonuçlanırlar. Tipik bir örnek, açık olduğu klasik Runge Kutta yöntemi bazen basit olarak adlandırılır için 4'ün Runge Kutta yöntemi: Birinci, dört yardımcı tesisi kullanılan olan ${\ görüntü stili k_ {1} = f (t_ {j}, y_ {j})}$${\ displaystyle k_ {2} = f (t_ {j} + h, y_ {j} + hk_ {1})}$${\ görüntü stili \ Phi}$${\ displaystyle {\ tfrac {1} {2}} k_ {1} + {\ tfrac {1} {2}} k_ {2}}$${\ görüntü stili s}$${\ displaystyle k_ {1}, \ dotsc, k_ {s}}$${\ görüntü stili f}$${\ görüntü stili \ Phi}$${\ displaystyle k_ {1}, k_ {2}, k_ {3}, \ dotsc}$

${\ displaystyle {\ başlangıç ​​{hizalanmış} k_ {1} & = f (t_ {j}, y_ {j}) \\ k_ {2} & = f (t_ {j} + {\ tfrac {h} {2 }}, y_ {j} + {\ tfrac {h} {2}} k_ {1}) \\ k_ {3} & = f (t_ {j} + {\ tfrac {h} {2}}, y_ {j} + {\ tfrac {h} {2}} k_ {2}) \\ k_ {4} & = f (t_ {j} + h, y_ {j} + hk_ {3}) \ bitiş {hizalı }}}$

ve sonra süreç eğimi olarak ağırlıklı ortalama

${\ displaystyle {\ tfrac {1} {6}} k_ {1} + {\ tfrac {1} {3}} k_ {2} + {\ tfrac {1} {3}} k_ {3} + {\ tfrac {1} {6}} k_ {4}}$

Kullanılmış. Bu iyi bilinen yöntem, Alman matematikçi Wilhelm Kutta tarafından 1901'de, Karl Heun'un bir yıl önce üç aşamalı tek aşamalı bir yöntem bulmasından sonra yayınlandı .

Mümkün olan en az sayıda aşama ile daha da yüksek dereceden açık süreçlerin inşası, matematiksel olarak çok zorlu bir problemdir. Şöyle John C. Butcher 1965 gösterebilmiştir, orada, örneğin, sırayla 5 için altı aşamalı prosedürlerin sadece minimum; 8. dereceden açık bir Runge-Kutta yöntemi en az 11 adım gerektirir. 1978'de Avusturyalı matematikçi Ernst Hairer , 17 adımlı 10. dereceden bir prosedür buldu . Böyle bir prosedür için katsayılar 1205 belirleyici denklemi sağlamalıdır. Örtük Runge-Kutta yöntemleri söz konusu olduğunda durum daha basit ve daha açıktır: her aşama sayısı için bir düzen yöntemi vardır ; bu aynı zamanda elde edilebilecek maksimum düzendir.${\ görüntü stili s}$${\ görüntü stili p = 2s}$

Ekstrapolasyon yöntemi

Ekstrapolasyon fikri, başlangıç ​​değer problemlerini tek adımlı yöntemlerle çözmekle sınırlı değildir, çözülecek sorunu bir adım boyutuyla ayrıklaştıran tüm sayısal yöntemlere benzer şekilde uygulanabilir . Bir ekstrapolasyon yönteminin iyi bilinen bir örneği , integrallerin sayısal hesaplanması için Romberg entegrasyonudur . Genel olarak, bu nedenle , bu makalenin durumunda, örneğin belirli bir noktada bir başlangıç ​​değer probleminin çözüm fonksiyonunun değeri, sayısal olarak belirlenecek bir değer olsun. Sayısal bir yöntem, örneğin tek adımlı bir yöntem , bunun için adım boyutunun seçimine bağlı olarak yaklaşık bir değer hesaplar . İşte, yöntem, yani yakınsak olduğu varsayılmıştır o karşı yakınsak ise sıfıra yakınsak. Bununla birlikte, bu yakınsama yalnızca tamamen teorik bir ifadedir, çünkü yöntemin gerçek uygulamasında, sonlu sayıda farklı adım boyutu için yaklaşık değerler hesaplanabilir, ancak elbette adım boyutunun "sıfıra yakınsamasına" izin veremezsiniz. Farklı aşama boyutunda için hesaplanan yaklaşımlar, ancak, (bilinmeyen) işlevi hakkında bilgi olarak anlaşılabilir : ekstrapolasyon olarak yöntem , bir interpolasyon polinom kullanılan bir şekilde yaklaştırılması, diğer bir deyişle bir polinom ile ${\ görüntü stili h}$${\ görüntü stili v}$${\ görüntü stili {\ tilde {v}} (h)}$${\ görüntü stili h> 0}$${\ görüntü stili {\ tilde {v}} (h)}$${\ görüntü stili v}$${\ görüntü stili h}$${\ displaystyle {\ tilde {v}} (h_ {1}), {\ tilde {v}} (h_ {2}), \ dotsc, {\ tilde {v}} (h_ {m})}$${\ displaystyle h_ {1}> h_ {2}> \ ldots> h_ {m}}$${\ görüntü stili {\ tilde {v}}}$${\ görüntü stili {\ tilde {v}}}$${\ görüntü stili P}$

${\ displaystyle P (h_ {k}) = {\ tilde {v}} (h_ {k})}$

için . Değeri noktasında polinom sonra olmayan hesaplanabilir sınırı için hesaplanabilir yaklaşım olarak kullanılmıştır için sıfıra doğru. Roland Bulirsch ve Josef Stoer , 1966'da ilk değer problemleri için erken başarılı bir ekstrapolasyon algoritması yayınladı .${\ görüntü stili k = 1,2, \ nokta nokta, m}$${\ görüntü stili P (0)}$${\ görüntü stili h = 0}$${\ görüntü stili {\ tilde {v}} (h)}$${\ görüntü stili h}$

Bir sipariş prosedüründe ekstrapolasyon${\ görüntü stili h = 0}$${\ görüntü stili p = 2}$

Tek adımlı bir sipariş yöntemi durumunda somut bir örnek , genel ekstrapolasyon prosedürünü anlaşılır kılabilir. Böyle bir yöntemle, küçük adım boyutları için hesaplanan yaklaşım, kolaylıkla formun bir polinomuna dönüştürülebilir. ${\ görüntü stili p}$${\ görüntü stili h}$

${\ displaystyle P (h) = a + bh ^ {p}}$

başlangıçta bilinmeyen parametrelerle ve yaklaşık değerlerle. Şimdi, iki yaklaşımı hesaplamak için ve bir adım boyutu ve adım boyutunun yarısı için prosedür kullanılırsa, enterpolasyon koşullarından ve bilinmeyenler için iki doğrusal denklem elde edilir ve . Tahmin edilen değer ${\ görüntü stili a}$${\ görüntü stili b}$${\ görüntü stili h_ {1}}$${\ displaystyle h_ {2} = {\ tfrac {1} {2}} h_ {1}}$${\ görüntü stili y_ {h_ {1}}}$${\ görüntü stili y_ {h_ {2}}}$${\ görüntü stili P (h_ {1}) = y_ {h_ {1}}}$${\ görüntü stili P (h_ {2}) = y_ {h_ {2}}}$${\ görüntü stili a}$${\ görüntü stili b}$${\ görüntü stili h = 0}$

${\ displaystyle P (0) = a = y_ {h_ {2}} + {\ frac {y_ {h_ {2}} - y_ {h_ {1}}} {2 ^ {p} -1}}}$

daha sonra genellikle başlangıçta hesaplanan iki değerden çok daha iyi bir yaklaşımı temsil eder. Bu şekilde elde edilen tek aşamalı işlemin sırasının en az , yani orijinal işlemden en az 1 daha büyük olduğu gösterilebilir.${\ görüntü stili p + 1}$

Adım boyutu kontrolü ile prosedür

Tek adımlı yöntemin bir avantajı , diğer adımlardan bağımsız olarak her adımda herhangi bir adım boyutunun kullanılabilmesidir. Pratikte bu açıkça nasıl seçileceği sorusunu gündeme getiriyor . Gerçek uygulamalarda her zaman bir başlangıç ​​değer probleminin çözümünün hesaplanacağı bir hata toleransı olacaktır; Örneğin , verilen problemin başlangıç ​​değerleri ve parametreleri için ölçüm hataları olan verilerden önemli ölçüde “daha ​​kesin” olan sayısal bir yaklaşım belirlemek anlamsız olacaktır . Bu nedenle amaç, bir yandan belirtilen hata toleranslarına bağlı kalınacak, ancak diğer yandan hesaplama eforunu küçük tutmak için mümkün olduğunca az adım kullanacak şekilde adım boyutlarını seçmek olacaktır. Genel olarak, bu ancak adım boyutları çözümün gidişatına uyarlanırsa başarılabilir: çözümün önemli ölçüde değiştiği küçük adımlar, neredeyse sabit olduğu büyük adımlar.${\ görüntü stili j}$${\ görüntü stili h_ {j}}$ ${\ görüntü stili h_ {j}}$

Durumunda iyi iklimlendirilmiş başlangıç değer problemleri, küresel usul hata yerel kesme hataların toplamına yaklaşık olarak eşit olduğu gösterilebilir tek adımda. Bu nedenle, seçilen tolerans eşiğinin altında olan mümkün olduğunca büyük bir adım boyutu seçilmelidir. Buradaki problem , noktasındaki başlangıç ​​değer probleminin bilinmeyen kesin çözümüne bağlı olduğu için doğrudan hesaplanamamasıdır . Bu nedenle, adım boyutu kontrolünün temel fikri , dayandığı temel yöntemden daha kesin bir yöntemle yaklaşmaktır.${\ displaystyle \ eta _ {j}: = \ | \ eta (t_ {j}, h_ {j}) \ |}$${\ görüntü stili h_ {j}}$${\ displaystyle \ eta _ {j}}$${\ displaystyle \ eta _ {j}}$${\ görüntü stili y (t_ {j})}$${\ görüntü stili t_ {j}}$${\ görüntü stili y (t_ {j})}$

Adım boyutu kontrolü için iki temel fikir, adım boyutunu ve gömülü prosedürleri yarıya indirmektir . Adım boyutunu yarıya indirirken, adım boyutunun yarısına sahip iki adımın sonucu, gerçek işlem adımına ek olarak bir karşılaştırma değeri olarak hesaplanır. Daha sonra için daha kesin bir yaklaşım, her iki değerden de ekstrapolasyon ile belirlenir ve böylece yerel hata tahmin edilir. Bu çok büyükse, bu adım atılır ve daha küçük bir adım boyutuyla tekrarlanır. Belirtilen toleranstan önemli ölçüde küçükse, bir sonraki adımda adım boyutu artırılabilir. Bu adım boyutu yarıya bölme yöntemi için ek hesaplama çabası nispeten büyüktür; bu nedenle, modern uygulamalar, adım boyutu kontrolü için çoğunlukla sözde gömülü yöntemleri kullanır. Temel fikir, farklı yakınsama derecelerine sahip iki tek adımlı yöntemi kullanarak her adım için iki yaklaşım hesaplamak ve böylece yerel hatayı tahmin etmektir. Hesaplama çabasını optimize etmek için, iki prosedürün mümkün olduğu kadar çok ortak hesaplama adımı olmalıdır: Bunlar “birbirine gömülmelidir”. Örneğin, gömülü Runge-Kutta yöntemleri aynı yardımcı eğimleri kullanır ve yalnızca ortalamaları açısından farklılık gösterir. İyi bilinen gömülü yöntemler, Runge-Kutta-Fehlberg yöntemlerini ( Erwin Fehlberg , 1969) ve Dormand-Prince yöntemlerini (JR Dormand ve PJ Prince, 1980) içerir.${\ görüntü stili y (t_ {j})}$${\ displaystyle \ eta _ {j}}$${\ görüntü stili y (t_ {j})}$

Pratik örnek: Sayısal yazılımla başlangıç ​​değeri problemlerini çözme

Bu makalede genel olarak sunulan matematiksel kavramlar için, kullanıcının pratik problemleri basit bir şekilde sayısal olarak çözmesini sağlayan çok sayıda yazılım uygulaması geliştirilmiştir. Somut bir örnek olarak, Lotka-Volterra denklemlerinin bir çözümü , yaygın olarak kullanılan sayısal yazılım Matlab ile hesaplanacaktır. Lotka-Volterra denklemleri, avcı ve av popülasyonları arasındaki etkileşimleri tanımlayan biyolojiden basit bir modeldir . Bunun için diferansiyel denklem sistemi verilmiştir.

${\ displaystyle {\ başlangıç ​​{hizalanmış} y_ {1} '(t) & = ay_ {1} (t) -by_ {1} (t) y_ {2} (t) \\ y_ {2}' (t ) & = cy_ {1} (t) y_ {2} (t) -dy_ {2} (t) \ end {hizalanmış}}}$

parametreler ve başlangıç ​​koşulu ile , . Burada ve av veya yırtıcı popülasyonun zamansal gelişimine karşılık gelir . Çözüm zaman aralığında hesaplanmalıdır. ${\ görüntü stili a = 1, b = 2, c = 1, d = 1}$${\ görüntü stili y_ {1} (0) = 3}$${\ görüntü stili y_ {2} (0) = 1}$${\ görüntü stili y_ {1}}$${\ görüntü stili y_ {2}}$${\ görüntü stili [0.20]}$

Matlab kullanılarak yapılan hesaplama için , diferansiyel denklemin sağ tarafındaki fonksiyon önce verilen parametre değerleri için tanımlanır : ${\ görüntü stili f}$${\ görüntü stili y '= f (t, y)}$

a = 1; b = 2; c = 1; d = 1;
f = @(t,y) [a*y(1) - b*y(1)*y(2); c*y(1)*y(2) - d*y(2)];

Ek olarak, zaman aralığı ve başlangıç ​​değerleri gereklidir:

t_int = [0, 20];
y0 = [3; 1];

Sonra çözüm hesaplanabilir:

[t, y] = ode45(f, t_int, y0);

Matlab işlevi ode45, adım boyutu kontrolü için yakınsama 4 ve 5 sıraları ile iki gömülü açık Runge-Kutta yöntemini kullanan tek adımlı bir yöntem uygular.

Çözüm artık mavi eğri ve kırmızı eğri olarak çizilebilir ; hesaplanan noktalar küçük dairelerle işaretlenmiştir: ${\ görüntü stili y_ {1}}$${\ görüntü stili y_ {2}}$

figure(1)
plot(t, y(:,1), 'b-o', t, y(:,2), 'r-o')

Sonuç, soldaki resimde aşağıda gösterilmiştir. Sağdaki resim, süreç tarafından kullanılan adım boyutlarını gösterir ve

figure(2)
plot(t(1:end-1), diff(t))

Lotka-Volterra denklemlerinin çözümleri

Kullanılan artışlar

Bu örnek, ücretsiz sayısal yazılım GNU Octave ile değişiklik yapılmadan da gerçekleştirilebilir . Ancak orada uygulanan yöntemle, biraz farklı bir adım boyutu sırası vardır.

Edebiyat

• John C. Butcher : Adi Diferansiyel Denklemler için Sayısal Yöntemler . John Wiley & Sons, Chichester 2008, ISBN 978-0-470-72335-7 . 
• Wolfgang Dahmen , Arnold Reusken: Mühendisler ve doğa bilimciler için sayısallar . 2. Baskı. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , bölüm. 11: Adi diferansiyel denklemler . 
• Peter Deuflhard , Folkmar Bornemann : Sayısal Matematik 2 - Adi Diferansiyel Denklemler . 3. Baskı. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 . 
• David F. Griffiths, Desmond J. Higham: Adi Diferansiyel Denklemler için Sayısal Yöntemler - İlk Değer Problemleri . Springer, Londra 2010, ISBN 978-0-85729-147-9 . 
• Robert Plato: Sayısal Matematik kompakt . 4. baskı. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , bölüm. 7: Başlangıç ​​değer problemleri için tek adımlı prosedür . 
• Hans-Jürgen Reinhardt: Adi diferansiyel denklemlerin sayısalları . 2. Baskı. Walter de Gruyter, Berlin / Boston 2012, ISBN 978-3-11-028045-6 . 
• Hans Rudolf Schwarz, Norbert Köckler: Sayısal Matematik . 8. baskı. Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1551-4 , bölüm. 8: Başlangıç ​​değer problemleri . 
• Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Adi diferansiyel denklemlerin sayısalları . 2. Baskı. Springer Spektrumu, Wiesbaden 2012, ISBN 978-3-8348-1847-8 . 

İnternet linkleri

• Lars Grüne: Adi Diferansiyel Denklemler için Sayısal Yöntemler (Sayısal Matematik II). (PDF) 2008, 20 Ağustos 2018'de erişildi (Bayreuth Üniversitesi'nden ders notları ). 
• Peter Spellucci: Adi diferansiyel denklemlerin sayısalları . (PDF) 2007, 20 Ağustos 2018'de erişildi ( TU Darmstadt'tan ders notları ). 
• Hans U. Fuchs: Diferansiyel Denklemler için Sayısal Yöntemler. (PDF) 2007, 20 Ağustos 2018'de erişildi (İngilizce, Zürih Uygulamalı Bilimler Üniversitesi'nden ders notları ). 
• Matematik dersi: birinci dereceden genel diferansiyel denklem hesaplayıcısı. İçinde: Matematik eğitimi. 20 Ağustos 2018'de alındı . 

Bireysel kanıt

1. ^ Thomas Sonar : 3000 Yıllık Analiz . Springer, Berlin / Heidelberg 2011, ISBN 978-3-642-17203-8 , s. 378-388 ve 401-426 . 
2. ↑ Jean-Luc Chabert ve diğerleri .: A History of Algorithms . Springer, Berlin / Heidelberg 1999, ISBN 978-3-540-63369-3 , s. 374-378 . 
3. ↑ Wolfgang Dahmen, Arnold Reusken: Mühendisler ve Bilim Adamları için Sayısal Analiz . 2. Baskı. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , s. 386 f . 
4. ↑ Wolfgang Dahmen, Arnold Reusken: Mühendisler ve Bilim Adamları için Sayısal Analiz . 2. Baskı. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , s. 386-392 . 
5. ↑ Hans Rudolf Schwarz, Norbert Köckler: Sayısal Matematik . 8. baskı. Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1551-4 , s. 350 f . 
6. ^ Robert Plato: Sayısal Matematik kompakt . 4. baskı. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , s. 157 . 
7. ^ Robert Plato: Sayısal Matematik kompakt . 4. baskı. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , s. 156 . 
8. ^ Robert Plato: Sayısal Matematik kompakt . 4. baskı. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , s. 157 . 
9. ↑ Hans-Jürgen Reinhardt: Adi diferansiyel denklemlerin sayısalları . 2. Baskı. Walter de Gruyter, Berlin / Boston 2012, ISBN 978-3-11-028045-6 , s. 42 f . 
10. ^ John C. Butcher: Adi Diferansiyel Denklemler için Sayısal Yöntemler . John Wiley & Sons, Chichester 2008, ISBN 978-0-470-72335-7 , s. 95-100 . 
11. ^ JC Butcher: 20. yüzyılda adi diferansiyel denklemler için sayısal yöntemler . İçinde: Hesaplamalı ve Uygulamalı Matematik Dergisi . bant 125 , hayır. 1-2 , 15 Aralık 2000, s. 21 f . ( çevrimiçi ). 
12. ↑ Peter Deuflhard, Folkmar Bornemann: Sayısal Matematik 2 - Adi diferansiyel denklemler . 3. Baskı. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 , s. 228 f . 
13. ↑ Peter Deuflhard, Folkmar Bornemann: Sayısal Matematik 2 - Adi diferansiyel denklemler . 3. Baskı. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 , s. 229-231 . 
14. ↑ Wolfgang Dahmen, Arnold Reusken: Mühendisler ve Bilim Adamları için Sayısal Analiz . 2. Baskı. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , s. 443 f . 
15. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Adi diferansiyel denklemlerin sayısalları . 2. Baskı. Springer Spektrumu, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 258 f . 
16. ↑ Jean-Luc Chabert ve diğerleri .: A History of Algorithms . Springer, Berlin / Heidelberg 1999, ISBN 978-3-540-63369-3 , s. 378 f . 
17. ↑ Jean-Luc Chabert ve diğerleri .: A History of Algorithms . Springer, Berlin / Heidelberg 1999, ISBN 978-3-540-63369-3 , s. 381-388 . 
18. ↑ Wolfgang Dahmen, Arnold Reusken: Mühendisler ve Bilim Adamları için Sayısal Analiz . 2. Baskı. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , s. 406 f . 
19. ^ JC Butcher: 20. yüzyılda adi diferansiyel denklemler için sayısal yöntemler . İçinde: Hesaplamalı ve Uygulamalı Matematik Dergisi . bant 125 , hayır. 1-2 , 15 Aralık 2000, s. 4-6 ( çevrimiçi ). 
20. ↑ Peter Deuflhard, Folkmar Bornemann: Sayısal Matematik 2 - Adi diferansiyel denklemler . 3. Baskı. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 , s. 160-162 . 
21. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Adi diferansiyel denklemlerin sayısalları . 2. Baskı. Springer Spektrumu, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 219-221 . 
22. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Adi diferansiyel denklemlerin sayısalları . 2. Baskı. Springer Spektrumu, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 79 ff . 
23. ^ JC Butcher: 20. yüzyılda adi diferansiyel denklemler için sayısal yöntemler . İçinde: Hesaplamalı ve Uygulamalı Matematik Dergisi . bant 125 , hayır. 1-2 , 15 Aralık 2000, s. 26 ( çevrimiçi ). 
24. ^ Robert Plato: Sayısal Matematik kompakt . 4. baskı. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , s. 171-173 . 
25. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Adi diferansiyel denklemlerin sayısalları . 2. Baskı. Springer Spektrumu, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 57-59 . 
26. ↑ Peter Deuflhard, Folkmar Bornemann: Sayısal Matematik 2 - Adi diferansiyel denklemler . 3. Baskı. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 , s. 199-204 . 
27. ^ Robert Plato: Sayısal Matematik kompakt . 4. baskı. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , bölüm. 7: Başlangıç ​​değer problemleri için tek adımlı yöntem , s. 173-177 . 
28. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Adi diferansiyel denklemlerin sayısalları . 2. Baskı. Springer Spektrumu, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 64-70 . 
29. ↑ ode45: Katı olmayan diferansiyel denklemleri çözün - orta dereceli yöntem. MathWorks, 23 Kasım 2017'de erişildi .